


¦rodek masy jest specyficznym punktem określającym bryłę. Gdyby bryłę można było traktować jako punkt to cała jej masa byłaby skupiona w punkcie środka masy. Punkt środka masy ma kolejną interesującą właściwość, mianowicie w jednorodnym polu grawitacyjnym pokrywa się on z punktem środka ciężkości. Jak wiadomo z prawa powszechnego ciążenia dwie masy przyciągają się wzajemnie. Ciało znajdujące się w polu grawitacyjnym Ziemi jest przyciągane nie tylko przez nią ale również przez pozostałe planety w układzie słonecznym oraz galaktyki znajdujące się w Wszechświecie. Oddziaływania grawitacyjne z innymi masami w Wszechświecie można pominąć z uwagi na ich zależność od kwadratu odległości pomiędzy masami.
Jak wspomniano powyżej środek ciężkości pokrywa się w środkiem masy gdy ciało znajduje się w jednorodnym polu grawitacyjnym. ¦rodek ciężkości ma bardzo ważną cechę. Bryła obrócona w jakikolwiek sposób wokół osi przechodzącej przez jej środek ciężkości pozostanie w równowadze.
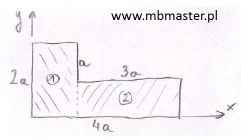
Wyznaczanie środka masy dla figury płaskiej o jednorodnym rozkładzie masy. Figura płaska jest obiektem dwuwymiarowym, oznacza to że środek masy będzie miał dwie współrzędne. Do rozpatrywanej figury przypisany zostanie dwuwymiarowy układ współrzędnych XY. W zadaniu figura płaska zostanie rozbita na dwie prostsze figury płaskie dla których możliwe jest wyznaczenie środka masy bezpośrednio z uwagi na ich symetryczną budowę. ¦rodek masy figury głównej zostanie wyznaczony z zastosowaniem wzorów ogólnych na środek masy.
¦rodek masy - zadanie 1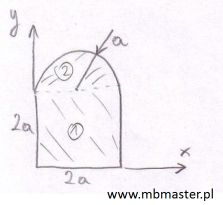
Wyznaczanie środka masy dla figury płaskiej o jednorodnym rozkładzie masy. Figura płaska jest obiektem dwuwymiarowym, oznacza to że środek masy będzie miał dwie współrzędne. Do rozpatrywanej figury przypisany zostanie dwuwymiarowy układ współrzędnych XY. Analizowana figura składa się z dwóch figur składowych. Pierwsza figura składowa to kwadrat, druga figura składowa to półkole. ¦rodek masy figury głównej zostanie wyznaczony z zastosowaniem wzorów ogólnych na środek masy.
¦rodek masy - zadanie 2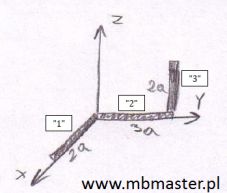
Wyznaczanie środka masy dla trójwymiarowej bryły. Bryła zbudowana jest z cienkiego pręta. Cienki pręt jest modelem obiektu jednowymiarowego. W analizowanym przykładzie pręt sformowany jest w taki sposób aby współrzędne jego środka masy opisane były w trójwymiarowym układzie współrzędnych XYZ (układ kartezjański). Znana jest gęstość liniowa pręta d[kg/m] oraz jego wymiary w każdym kierunku układu współrzędnych.
¦rodek masy - zadanie 3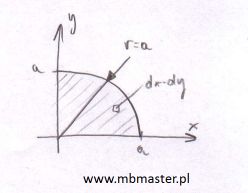
Wyznaczanie środka masy dla ćwiartki koła. Masa rozłożona jest jednorodnie na ćwiartce koła. Znana jest gęstość powierzchniowa d[kg/m2] masy rozłożonej na ćwiartce koła. Do figury przypisany zostanie dwumiarowy układ współrzędnych XY. W celu wyznaczenia współrzędnych środka ciężkości obliczona zostanie całka podwójna w układzie biegunowym rφ. Z uwagi na symetrię wartości współrzędnych środka masy dla ćwiartki koła w tak przypisanym układzie współrzędnych będą takie same xC=yC.
¦rodek masy ćwiartki koła - zadanie 4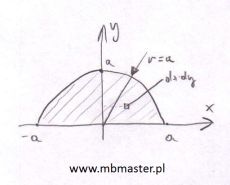
Wyznaczanie środka masy dla półkola. Masa rozłożona jest jednorodnie na półkolu. Znana jest gęstość powierzchniowa d[kg/m2] masy rozłożonej na półkolu. Do figury przypisany zostanie dwumiarowy układ współrzędnych XY. W celu wyznaczenia współrzędnych środka ciężkości obliczona zostanie całka podwójna w układzie biegunowym rφ. Z uwagi na symetrię półkola w tak przypisanym układzie współrzędnych, współrzędna xC środka masy możliwa jest do wyznaczenia wprost.
¦rodek masy półkola - zadanie 5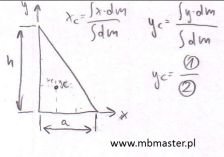
Wyznaczanie środka masy dla trójkąta prostokątnego. Znana jest wysokość trójkąta h[m] oraz jego podstawa a[m]. Masa rozłożona jest jednorodnie na trójkącie prostokątnym. Znana jest gęstość powierzchniowa d[kg/m2] masy rozłożonej na trójkącie. Do figury przypisany zostanie dwumiarowy układ współrzędnych XY. W celu wyznaczenia współrzędnych środka ciężkości obliczona zostanie całka podwójna. Najpierw zostanie wyznaczona współrzędna yC środka masy. Współrzędna xC środka masy zostanie wyznaczona w oparciu o analogię, ponieważ dla współrzędnej x będzie możliwe potraktowanie trójkąta tak aby jego podstawa była jego wysokością a wysokość jego podstawą.
¦rodek masy trójkąta prostokątnego - zadanie 6