Transmitancja operatorowa jest jednym z rodzajów modeli matematycznych obiektów.

Transmitancję operatorową G(S) definiujemy jako stosunek transformaty Laplace’a sygnału wyjściowego Y(s) do transformaty Laplace’a sygnału wejściowego U(s). Model matematyczny obiektu w postaci transmitancji operatorowej łączy w jednym równaniu zależność miedzy sygnałem wejściowym a sygnał wyjściowym. Znając transmitancję operatorową obiektu można wyznaczyć jego odpowiedź na zadane wymuszenie. Sygnałami wejściowymi i wyjściowymi mogą być różne wielkości fizyczne. W przypadku układów elektrycznych sygnałem wejściowym może być napięcie U a sygnałem wyjściowym prąd I. W układach mechanicznych sygnałem wejściowym może być siła F a sygnałem wyjściowym przesunięcie δx. Modelowany obiekt może być też hybrydą, czyli połączeniem układu mechanicznego i elektrycznego. W przypadku obiektu elektromechanicznego sygnałem wejściowym może być napięcie U a sygnałem wyjściowym moment M. Przykładem obiektu elektromechanicznego jest silnik indukcyjny. W rozwiązanych zadaniach zamieszczonych poniżej wyznaczana jest transmitancja operatorowa dla różnych obiektów elektrycznych i mechanicznych.

Transmitancja operatorowa – zadanie 1

Wyznaczanie transmitancji operatorowej G(s) dla czwórnika. Obwód elektryczny zbudowany jest z trzech elementów: kondensatora C, rezystora R₁ i rezystora R₂. W celu wyznaczenia transmitancji zapisujemy prądy i napięcia w postaci operatorowej, następnie zapisujemy równania dla pierwszego i drugiego prawa Kirchhoffa. W oparciu o równania Kirchhoffa wyznaczamy transmitancję operatorową obiektu.
Transmitancja operatorowa układu elektrycznego 1

Transmitancja operatorowa – zadanie 2

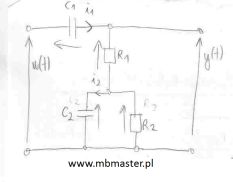
Wyznaczanie transmitancji operatorowej G(s) dla czwórnika. Obwód elektryczny złożony jest z czterech elementów: kondensatorów C₁ i C₂, oraz rezystorów R₁ i R₂. W celu wyznaczenia transmitancji zapisujemy prądy i napięcia w postaci operatorowej, następnie zapisujemy równania dla pierwszego i drugiego prawa Kirchhoffa. W oparciu o równania Kirchhoffa wyznaczamy transmitancję operatorową obiektu.
Transmitancja operatorowa układu elektrycznego 2

Transmitancja operatorowa – zadanie 3

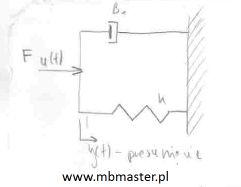
Rozwiązany przykład z wyznaczaniem transmitancji operatorowej G(s) dla układu mechanicznego. Układ mechaniczny zbudowany jest z połączonych równolegle elementów takich jak sprężyna i tłumik wiskotyczny. Sprężyna posiada parametr k[N/m] opisujący jej sztywność, tłumik wiskotyczny opisany jest parametrem B[N·s/m]. Układ poddany jest wymuszeniu u(t) w postaci siły F. Sygnałem wyjściowym jest przemieszczenie elementów y(t). Sygnał wejściowy i wyjściowy zostają zapisane w postaci operatorowej w celu wyznaczenia transmitancji.
Transmitancja operatorowa układu mechanicznego 1

Transmitancja operatorowa – zadanie 4

Dla obiektu mechanicznego wyznaczona zostanie transmitancja operatorowa G(s). Obiekt mechaniczny zbudowany jest z masy m. Masa osadzona jest na podłożu poprzez tłumik o stałej konstrukcyjnej B[N·s/m] połączony równolegle z sprężyną o sztywności k₂[N/m]. Od góry do masy przymocowana jest sprężyna o sztywności k₁[N/m]. Sprężyna k₁ zostaje ściśnięta o odległość u(t). Odległość u(t) jest sygnałem wejściowym. W wyniku przemieszczenia się sprężyny k₁ środek ciężkości masy przemieszcza się o odległość y(t). Przemieszczenie środka masy jest sygnałem wyjściowym. Dla obiektu zostaje zapisane równanie ruchu w postaci operatorowej. W oparciu o równanie ruchu wyznaczona zostaje transmitancja operatorowa. Transmitancja operatorowa układu mechanicznego 2

Transmitancja operatorowa – zadanie 5

Dla obiektu mechanicznego wyznaczona zostanie transmitancja operatorowa G(s). Obiekt mechaniczny zbudowany jest z dwóch wózków, większy wózek posiada masę m₁[kg], mniejszy wózek posiada masę m₂[kg]. Mniejszy wózek znajduję się wewnątrz większego wózka i jest przymocowany do jednej z jego ścianek za pomocą sprężyny o stałej k[N/m]. Sygnałem wejściowym jest przesunięcie dużego wózka. Na skutek działania sygnału wejściowego duży wózek porusza się w prawo. Sygnałem wyjściowym jest przesunięcie małego wózka. Tarcie i opór powietrza są pominięte w przykładzie.
Transmitancja operatorowa układu mechanicznego 3

Transmitancja operatorowa – zadanie 6

Dla obiektu mechanicznego wyznaczona zostanie transmitancja operatorowa G(s). Obiekt mechaniczny zbudowany jest z dwóch wózków, większy wózek posiada masę m₁[kg], mniejszy wózek posiada masę m₂[kg]. Mniejszy wózek znajduję się wewnątrz większego wózka i jest przymocowany do jednej z jego ścianek za pomocą sprężyny o stałej k[N/m]. Sygnałem wejściowym jest przesunięcie dużego wózka. Na skutek działania sygnału wejściowego duży wózek porusza się w lewo. Sygnałem wyjściowym jest przesunięcie małego wózka. Tarcie i opór powietrza są pominięte w przykładzie.
Transmitancja operatorowa układu mechanicznego 4

Transmitancja operatorowa – zadanie 7

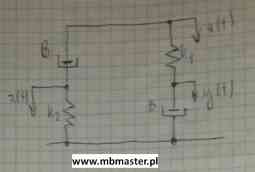
Obiekt automatycznej regulacji zbudowany jest z dwóch sprężyn k₁, k₂ oraz dwóch tłumików wiskotycznych B. Elementy składowe obiektu regulacji połączone są z sobą równolegle. Konfiguracja połączenia elementów jest zamieszczona na rysunku. Dla rozpatrywanego układu wyznaczona zostanie transmitancja operatorowa G(s). W przykładzie warunki początkowe są równe zeru.
Transmitancja operatorowa układu mechanicznego 5