Macierz rotacji i kąty Eulera

SKOCZ DO:
macierz rotacji - zadanie 1
kąty Eulera - zadanie 1
kąty Eulera - zadanie 2
kąty Eulera - zadanie 3

Macierz rotacji opisuje rotację pomiędzy jednym układem współrzędnych a drugim układem współrzędnych w ogólności macierz rotacji przedstawiająca transformację współrzędnych z układu {B} do układu {A} jest postaci:

macierz rotacji z układu {B} do układu {A}

Jak widać na rysunku powyżej macierz rotacji jest macierzą iloczynów skalarnych wersorów kolejnych osi układów współrzędnych {A} i {B}.

Kąty Eulera opisują dowolną rotację pomiędzy układami współrzędnych kartezjańskich. W ogólności każdą rotację można przedstawić jak złożenie trzech obrótów pomiędzy układami współrzędnych. Każdy z obrotów składowych jest rotacją wokół jednej z osi. W rozważanych tutaj przykładach obroty bedą następować kolejno wokół osi Z-Y-X. Tok postępowania podczas rotacji jest następujący
• Pierwszy obrót następuje wokół osi Z_A układu wejściowego i odbywa sie w płaszczy�znie X_AY_A o kąt ψ, w efekcie powstaje układ {B'}, osie Z_A i Z_B' pokrywają się.
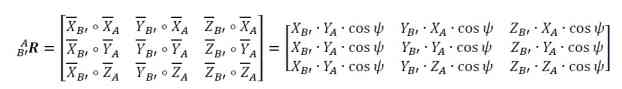
macierz rotacji z układu {B'} do układu {A}
• Drugi obrót następuje wokół osi Y_B' układu {B'} i odbywa sie w płaszczy�znie X_B'Z_B' o kąt θ, w efekcie powstaje układ {B''}, osie Y_B'' i Y_B' pokrywają się.
macierz rotacji z układu {B''} do układu {B'}
• Trzeci obrót następuje wokół osi X_B'' układu {B''} i odbywa sie w płaszczy�znie Y_B''Z_B'' o kąt φ, w efekcie powstaje układ wyjściowy {B}, osie X_B i X_B' pokrywają się.
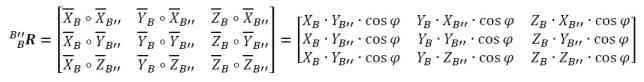
macierz rotacji z układu {B} do układu {B''}
W ogólności macierz z układu {B} do {A} jest równa iloczynowi trzech macierzy.

Macierz rotacji - zadanie 1

W układzie współrzędnych kartezjańskich {B} znajduje się wektor ^BP. Współrzędne wektora ^BP określone są w układzie {B}. Początek układu współrzędnych {B} jest przeunięty względem początku układu współrzędnych {A} o wektor ^AP_BORG. Układ {B} jest także obrócony względem układu {A} wokół osi Y o kąt Θ=π/6. Celem w zadaniu jest wyznaczenie pozycji wektora P w układzie {A} → ^AP. Pozycja wektora P w układzie {A} jest równa iloczynowi macierzy rotacji z układu {B} do układu {A} z wektorem ^BP plus wektor ^AP_BORG.

Macierz rotacji - zadanie 1

Kąty Eulera i macierze rotacji - zadanie 1

Układ współrzędnych {B} jest obrócony względem układu współrzędnych {A} wokół każdej z osi według kolejności Z-Y-X. Kąty Eulera dla tak wykonanych obrotów wynoszą kolejno: ψ=π/2, θ=π/2, φ=π/2. W zadaniu wyznaczone zostaną kolejne macierze rotacji pomiędzy pośrednimi układami współrzędnych. Najpierw z układu współrzędnych {B} → {B''}, następnie z układu współrzędnych {B''} → {B'}, następnie z układu współrzędnych {B'} → {A}.

Kąty Eulera i macierze rotacji - zadanie 1

Kąty Eulera i macierze rotacji - zadanie 2

Układ współrzędnych {B} jest obrócony względem układu współrzędnych {A} wokół każdej z osi według kolejności Z-Y-X. Kąty Eulera dla tak wykonanych obrotów wynoszą kolejno: ψ=π/3, θ=2·π/3, φ=3·π/2. W zadaniu wyznaczone zostaną kolejne macierze rotacji pomiędzy pośrednimi układami współrzędnych. Najpierw z układu współrzędnych {B} → {B''}, następnie z układu współrzędnych {B''} → {B'}, następnie z układu współrzędnych {B'} → {A}.

Kąty Eulera i macierze rotacji - zadanie 2

Kąty Eulera i macierze rotacji - zadanie 3

Układ współrzędnych {B} jest obrócony względem układu współrzędnych {A} wokół każdej z osi według kolejności Z-Y-X. Kąty Eulera dla tak wykonanych obrotów wynoszą kolejno: ψ=π/4, θ=2·π/8, φ=3·π/2. W zadaniu wyznaczone zostaną kolejne macierze rotacji pomiędzy pośrednimi układami współrzędnych. Najpierw z układu współrzędnych {B} → {B''}, następnie z układu współrzędnych {B''} → {B'}, następnie z układu współrzędnych {B'} → {A}.

Kąty Eulera i macierze rotacji - zadanie 3