Znaleźć tutaj można szereg zadań z mechaniki jakie spotkać można podczas studiów wyższych. Rozwiązane są tutaj przykłady z statyki, kinematyki i dynamiki. Zamieszczone są tutaj kompletne rozwiązane przykłady z wytrzymałości materiałów. Przykłady z wytrzymałości materiałów związane są z naprężeniami w belkach, naprężeniami w prętach, naprężeniami w wałach oraz obliczaniem momentów bezwładności.
Wersja anglojęzyczna:
Mechanical engineering

Mechanika statyka:

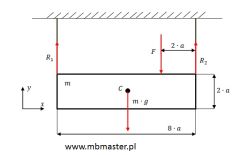
Rozwiązane zadania i przykłady z statyki. W statyce badamy wpływ sił na ciała znajdujące się spoczynku. W statyce ruch nie występuje. Ciała poddane działaniom sił zewnętrznych lub momentów sił zewnętrznych znajdują się w równowadze. Równowaga jest zapewniona poprzez siły reakcji. Siły reakcji wprowadzone są w momencie uwolnienia ciała od więzów. Najprostszym przykładem siły reakcji jest siła nacisku. W polu grawitacyjnym na każde ciało działa siła ciężkości, często nazywana ciężarem. Jeżeli przedmiot leży na podłodze to naciska na nią swoją siłą ciężkości, która jest kierowana pionowa w dół. Jeżeli chcemy dany przedmiot uwolnić od podłogi to musimy uwzględnić na mocy trzeciej zasady dynamiki Newtona (zasady akcji i reakcji) siłę z jaką podłoga działa na przedmiot. Siła z którą podłoga działa na przedmiot jest siłą nacisku i jest przeciwnie skierowana do ciężaru. Gdybyśmy po uwolnieniu od więzów nie wprowadzili tej siły to na mocy pierwszej zasady dynamiki na ciało działaby niezrównoważona siła, która powinna powodować ruch ciała z przyśpieszeniem a. Wartość przyśpieszenia jest związana z siłą wymuszającą druga zasadą dynamiki. Gdyby siła nacisku nie została wprowadzona to ciało nie znajdowałoby się w spoczynku, co nie jest zgodne rzeczywistością.

Mechanika statyka – zadania

Mechanika kinematyka:

Kinematyka jest działem mechaniki. W kinematyce zajmujemy się tylko i wyłącznie badaniem ruchu. Nie zajmuje się przyczynami ruchu, zajmujemy się samym ruchem. Na stronie zamieszczone są różne przykłady w których obliczane są prędkości, przyśpieszenia, droga, czas, energia podczas różnych przypadków ruchu. Istnieje wiele rodzajów ruchu, który można na różne sposoby klasyfikować. Mamy więc ruch jednostajny oraz ruch przyśpieszony, które sklasyfikowane są względu na zmienność prędkości w czasie. Istnieje także ruch prostoliniowy oraz ruch krzywoliniowy, które są sklasyfikowane ze względu na kształt toru ruchu. W mechanice często spotykamy się także z ruchem po okręgu oraz ruchem płaskim. Ruch płaski to złożenie ruchu postępowego i obrotowego bryły sztywnej. Odmian ruchu jest kilka, zamieszczone tu zadania będą starały się pokazać chociaż po jednym z nich.

Mechanika kinematyka – zadania

Mechanika dynamika:

Dynamika jest działem mechaniki. W dynamice badamy w jaki sposób siły wpływają na ciało oraz na jego ruch. W dynamice posługujemy się zasadami dynamiki Newtona. Znajomość zasad dynamiki Newtona jest więc podstawą do poprawnego rozwiązywania zagadnień dynamiki. Jako przypomnienie przedstawimy te zasady.

⋅ Pierwsza zasada dynamiki – Jeżeli na ciało nie działa żadna siła lub siły działają, ale się równoważą to ciało to pozostaje w spoczynku lub porusza się ruchem jednostajnym z prędkością v.
⋅ Druga zasada dynamiki – Jeżeli na ciało działa niezrównoważona siła to ciało to porusza się ruchem jednostajnie przyśpieszonym. Przyśpieszenie tego ruchu jest wprost proporcjonalne do działającej siły a odwrotnie proporcjonalne do masy ciała → a=F/m.
⋅ Trzecia zasada dynamiki – Jeżeli ciał A działa na ciało B siłą F_AB to również ciało B działa na ciało A siłą F_BA równą co do wartości lecz przeciwnie skierowaną → F_AB=-F_BA. Zasada ta jest często spotykana pod nazwą zasady akcji i reakcji.

Mechanika dynamika – zadania

Mechanika tarcie

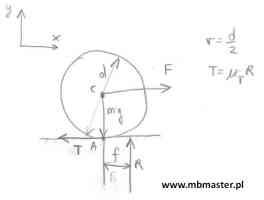
Zjawisko tarcia jest jednym z podstawowych oporów ruchu z jakim spotykamy się w mechanice. Tarcie jest oporem materii, która przeciwdziała ruchowi ciała umieszczonego w niej. Opór powietrza jest przykładem oporu materii. W mechanice najczęściej spotykamy się z dwoma rodzajami tarcia: tarciem przesuwnym (siła tarcia powstaje w wyniku przesuwania się po sobie powierzchni lub próby przesunięcia bez wykonania wprowadzenia w ruch) i tarciem tocznym (opór podczas toczenia ciał). Gdy tarcie nie występowało to na mocy pierwszej zasady dynamika Newtona ciało raz rozpędzone poruszałoby się ruchem jednostajnym w nieskończoność, gdyby na ciało działała niezrównoważona siła to na mocy drugiej zasady dynamiki Newtona ciało rozpędzałoby się w nieskończoność. Oczywiście jak wiemy z doświadczeń oba hipotetyczne przypadki nie występują. Pierwszy przypadek jest niemożliwy z uwagi na występowanie oporu materii, a drugi przypadek z powodu oporu materii oraz ograniczeń związanych Szczególną Teorią Względności Alberta Einsteina (żadne ciało posiadające masę spoczynkową większą od zera, nie może osiągnąć prędkości większej od prędkości światła c w próżni).
Tarcie opisane jest prawami tarcia. Prawa tarcia zostały wyznaczone doświadczalnie.
• siła tarcia jest zawsze przeciwna do występującego lub zakładanego kierunku ruchu
• wartość siły tarcia nie zależy od pola powierzchni stykających się ciał, zależy od rodzaju tych powierzchni
• siła tarcia T związana jest siłą nacisku N równaniem T=μ·N
• dla małych prędkości względnych, siła tarcia jest niezależna od prędkości

Tarcie przesuwne podzielone jest na:
• tarcie przesuwne statyczne μ_s[-]
• tarcie przesuwne kinetyczne opisane współczynnikiem μ_k[-]
Jak można wnioskować z nazewnictwa rodzajów tarć przesuwnych, przy tarciu przesuwnym statycznym ruch nie występuje μ_s[-], natomiast tarcie przesuwne kinetyczne μ_s[-] występuje podczas ruchu. Współczynniki tarć przesuwnych są bezwymiarowe, ich wartości wyznaczane są doświadczalnie. Wartości współczynników tarcia dla różnych materiałów znaleźć można tablicach matematyczno-fizycznych. Zapamiętać należy fakt, że współczynnik tarcia przesuwnego statycznego ma zawsze większe wartość od współczynnika tarcia przesuwnego kinetycznego → μ_s>μ_k. Źródłem siły tarcia są „szczątkowe” oddziaływania elektromagnetyczne pomiędzy molekułami (atomami) stykających się powierzchni. Siła tarcia ma zawsze przeciwnym zwrot do kierunku ruchu ciała, bądź zakładanego kierunku ruchu ciała.
Tarcie toczne (tarcie potoczyste) występuje podczas toczenia się ciał. Tarcie toczne występuje podczas toczenia, jest ono wynikiem odkształcania się stykających powierzchni podczas toczenia. Tarcie toczne opisane jest współczynnikiem ƒ[m]. Współczynnik tarcia tocznego nie jest wielkością bezwymiarową, posiada on wymiar a jest nim metr. W wyniku tarcia tocznego następuje przesunięcie siły nacisku N o odległość ƒ kierunku równoległym do siły nacisku jakby toczenie nie występowało. Siła nacisku N jest przesuwana o współczynnik tarcia tocznego ƒ w zakładanym kierunku występowania ruchu. Dzieląc współczynnik tarcia tocznego ƒ przez promień r toczącego się ciała można wprowadzić bezwymiarowy współczynik oporu przy toczeniu (współczynnik ten obowiązuje tylko dla danego promienia r) → (ƒ/r)=μ_t(r). Pomiędzy wprowadzonym przed chwilą bezwymiarowym współczynnikiem tarcia tocznego μ_t(r) a współczynnikami dla tarcia przesuwnego zachodzi nierówność μ_t(r)<μ_k<μ_s. Z nierówności wynika, że siła tarcia podczas toczenia jest zawsze mniejsza od tarcia przesuwnego(ślizgowego), tłumaczy to dlaczego od niepamiętnych czasów toczeniem zastępowano przesuwanie. Dla napędów wykorzystujących ruch obrotowy z siłą tarcia związany jest moment obciążający będący momentem biernym, ponieważ jego zwrot zależy od kierunku ruchu M_T=f(ω).

Mechanika tarcie – zadania

Drgania harmoniczne

Drgania harmoniczne są jednym z podstawowych zjawisk z jakimi mamy do czynienie w przyrodzie. W bardzo dużym skrócie można powiedzieć, ze wszystko drga. Każde ciało stałe wykonuje drgania, których częstotliwość nazywa się częstotliwością drgań własnych. Gdyby zacząć działać na ciało siłą wymuszającą o częstotliwości równej częstotliwości drgań własnych ciała to doprowadzi się je do zjawiska rezonansu mechanicznego. Oczywiście zjawisko rezonansu nie jest zarezerwowane tylko dla oddziaływań mechanicznych, występuje ono również w innych oddziaływaniach fizycznych. Przykładem jest rezonans elektryczny, szeroko stosowany w radioodbiornikach. Praktyczne jego zastosowanie polega na zwiększaniu się amplitudy interesującego nas sygnału dla sprecyzowanej częstotliwości. Układ wykonujący drgania harmoniczne porusza ruchem harmonicznym. Gdy siła działająca na ciało jest wprost proporcjonalna do wychylenia od pozycji równowagi to dany obiekt porusza się ruchem harmonicznym.

Drgania harmoniczne zadania

Zadania i przykłady z wytrzymałości materiałów

Na stronie znaleźć można sporo przykładów z wytrzymałości materiałów. Zamieszczone są tu przykłady rozwiązane od podstaw.
Wśród przykładów są zadania z belką, zadania z wałem oraz zdania z przekrojami.

Zadania z belką – przykłady:

Wyznaczanie momentów gnących i sił poprzecznych(sił tnących) w belkach. Przykłady zaczynają się od wyznaczenia równań równowagi statycznej znanych z statyki. Następnym krokiem w przykładach jest obliczenie wartości sił i reakcji w belkach po uwolnieniu ich od więzów. W oparciu o uzyskane wyniki dokonujemy analizy wytrzymałościowej rozpatrywanych układów mechanicznych. Wyznaczone zostają charakterystyki momentu gnącego i siły poprzecznej na całej długości belki. Często zastosowanie znajduje również prawo Hooke’a za pomocą którego wyznaczone zostają minimalne przekroje zapewniające przeniesienie obciążeń.

Naprężenia w belkach zadania

Zadania z prętami – przykłady:

Podczas wyznaczania naprężeń w prętach lub układach prętów stosujemy prawo Hooke’a. Prawo Hooke’a łączy w jednym równaniu zmianę długości pręta Δl[m] z siłą P[N] powodującą tą zmianę. Bezwzględnie należy jednak pamiętać kiedy można zastosować prawo Hooke’a. Prawo Hooke’a obowiązuje do granicy proporcjonalności materiału σ_H. Jak wiadomo z wytrzymałości materiałów do granicy proporcjonalności danego materiału zależność pomiędzy naprężeniami σ[Pa] a odkształceniami względnymi ε[-] jest liniowa. Charakterystyka przedstawiająca zależność naprężeń w funkcji odkształceń względnych nazywa się krzywą naprężania. Krzywa naprężania ma dla różnych materiałów różny przebieg. Przebieg funkcji σ=f(ε) jest otrzymywany empirycznie, czyli w skutek doświadczenia.

Naprężenia w prętach – zadania

Zadanie z wałem – przykłady:

Rozwiązane zadania z wytrzymałości materiałów dotyczące wyznaczania naprężeń w wałach mechanicznych. W zadaniach obliczane są momenty gnące M_g oraz momenty skręcające M_s w różnych układach obciążenia wału. W zadaniach zastosowana jest hipoteza Hubera do wyznaczenia momentu zredukowanego obciążającego wał. W każdym zadaniu wyznaczone są równania równowagi statycznej. Rozpatrywane przykłady wyznaczające naprężenia w wałach są trójwymiarowe. Siły lub składowe sił obciążające wały skierowane wzdłuż każdej z osi kartezjańskiego układu współrzędnych X-Y-Z. Równowaga statyczna układów opisana będzie układem sześciu równań. Trzy równania będą dotyczyły równowagi sił w kierunkach osi X, Y, Z. Pozostałe trzy równania będą dotyczyły równowagi momentów sił wokół osi X, Y, Z.

Wyznaczanie momentów gnących, momentów skrętnych oraz naprężeń w wałach mechanicznych – zadania

Wyznaczanie środków masy – zadania

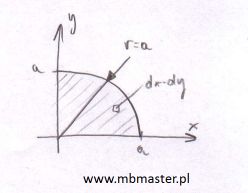
Środek masy jest specyficznym punktem określającym bryłę. Gdyby bryłę można było traktować jako punkt to cała jej masa jest skupiona w punkcie środka masy. Punkt środka masy kolejną interesującą właściwość, mianowicie w jednorodnym polu grawitacyjnym pokrywa się on z punktem środka ciężkości. Jak wiadomo z prawa powszechnego ciążenia dwie masy przyciągają się wzajemnie. Ciało znajdujące się w polu grawitacyjnym Ziemi jest przyciągane nie tylko przez nią ale również przez pozostałe planety w układzie słonecznym oraz galaktyki znajdujące się w Wszechświecie. Oddziaływania grawitacyjne z innymi masami w Wszechświecie można pominąć z uwagi na ich zależność od kwadratu odległości pomiędzy masami.
Jak wspomniano powyżej środek ciężkości pokrywa się w środkiem masy gdy ciało znajduje się w jednorodnym polu grawitacyjnym. Środek ciężkości ma bardzo ważną cechę. Bryła obrócona w jakikolwiek sposób wokół osi przechodzącej przez jej środek ciężkości pozostanie w równowadze.

Środek masy – zadania

Momenty bezwładności – zadania

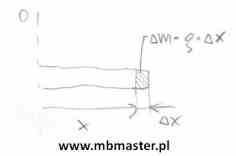
Moment bezwładności jest odpowiednikiem masy w ruchu obrotowym bryły sztywnej. Moment bezwładności opisuje rozkład masy bryły wokół osi obrotu. W przypadku punktu materialnego o masie m wyznaczenie jego momentu bezwładności jest stosunkowo proste. Moment bezwładności dla punktu materialnego obracającego się wokół osi oddalonej o odległość r jest dany równaniem I=m·r². Jak można wnioskować z równania na moment bezwładności posiada on jednostkę a jest nią [kg·m². W przypadku ogólnym do wyznaczenia momentu bezwładności stosuje się rachunek całkowy. Wzór ogólny na moment bezwładności jest dany równaniem

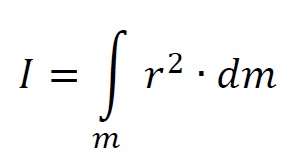
Momenty bezwładności podstawowych brył dla osi obrotów przechodzących przez ich środki symetrii zostały obliczone. Często jednak konieczne jest obliczenie momentu bezwładności bryły dla innej osi obrotu. Obliczenie momentu bezwładności dla osi obrotu równoległej do osi symetrii i oddalonej o odległość d jest możliwe poprzez zastosowanie twierdzenia Steinera o osiach równoległych.

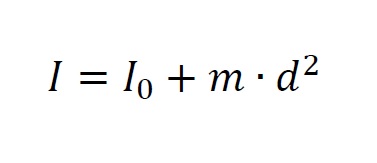
Momenty bezwładności – zadania

Momenty bezwładności i środki ciężkości – zadania

Wyznaczanie momentów bezwładności i środków ciężkości dla różnych układów brył. Środek ciężkości jest punktem będącym środkiem masy bryły do którego przyłożona jest siła ciężkości. Środek ciężkości ma jedną szczególną właściwość, bryła w jakikolwiek sposób obrócona wokół osi przechodzącej przez jej środek pozostanie w równowadze. Wyznaczanie środków masy dla niezłożonych brył o równomiernym rozkładzie masy (w każdym swoim punkcie maja taką samą gęstość) jest zadaniem prostym → przykładami są sześcian lub kula. W przypadku bardziej złożonych brył zadanie jest już trudniejsze.
Moment bezwładności jest odpowiednikiem masy w ruchu obrotowym. W ogólności moment bezwładności jest równy
I=∫r²·dm
gdzie
• r – odległość masy od osi obrotu [kg]
• dm – elementarna masa [m]
Jednostką momentu bezwładności jest [kg·m²]. Podczas wyznaczania momentów bezwładności rozmaitych figur bardzo często posługujemy się twierdzeniem Steinera o osiach równoległych.
Twierdzenie Steinera:
I=I₀+m·d²
gdzie
• I₀ – moment bezwładności bryły dla osi przechodzącej przez jej środek ciężkości [kg·m²]
• I – moment bezwładności dla dowolnej osi równoległej do osi przechodzącej przez środek ciężkości bryły [kg·m²]
• d – odległość między osiami [m]
• m – masa bryły [m]
Jak można zauważyć z twierdzenia Steinera nasuwa się prosty wniosek że bryła ma zawsze najmniejszy moment bezwładności dla osi przechodzącej przez jej środek ciężkości.

Momenty bezwładności i środki ciężkości – zadania

Mechanika płynów

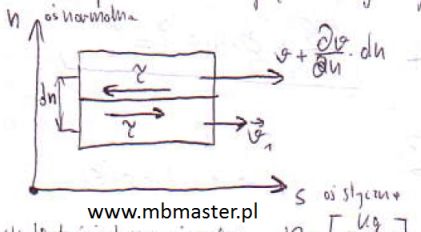
Zbiór notatek z mechaniki płynów zawierający informacje o: lepkości – prawo tarcia Newtona, pochodna substancjalna, pochodna wektora pola, zasada zachowania masy (równanie ciągłości przepływu), równanie pędu (równanie Eulera), reakcja hydrodynamiczna, zasada zachowania krętu w przepływie, zasada zachowania energii w przepływie – równanie Bernoulliego, zasada działania rurek spiętrzających, równanie Naviera-Stokesa – przepływ płynu rzeczywistego, przepływ laminarny.

Mechanika plynow