


Proste zadanie kinematyki polega wyznaczaniu wektora pozycji danego punktu w układzie kartezjańskim, którym najczęściej jest układ bazowy. W prostym zadaniu kinematyki znane są kąty ugięcia Θi (człon obrotowy) oraz przesunięcia danych członów di (człon przesuwny). W oparciu o znajomość tych wielkości wyznaczamy współrzędne kartezjańskie wektora pozycji w danym układzie współrzędnych. Proste zadanie kinematyki polega na przejściu z przestrzeni zmiennych przegubowych do przestrzeni kartezjańskiej. W skrócie proste zadanie kinematyki można symbolicznie jako:
{Θi,di} → {Xi,Yi,Zi}
Rozwiązanie kinematyki prostej manipulatora(robota) polega na zapisaniu tabelki parametrów zgodnie z notacją Denavita-Hartenberga. Następnie w oparciu o uzyskane parametry i postać ogólną macierzy transformacji ii-1T z układu "i" do "i-1" tworzy się macierze transformacji pomiędzy kolejnymi układami współrzędnych.
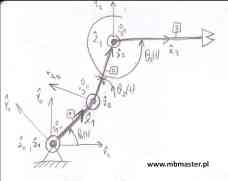
Rozwiązanie prostego zadania kinematyki dla manipulatora RRR. Manipulator RRR to robot posiadający trzy przeguby obrotowe. W przykładzie wyznaczona zostanie tabelka parametrów zgodnie z notacją Denavita-Hartenberga. Następnie w oparciu o wyznaczone parametry z tabelki wyznaczone zostaną macierze transformacji pomiędzy kolejnymi układami współrzędnych związanych z robotem. Z manipulatorem RRR związane są trzy układy współrzędnych, wyznaczone zostaną więc trzy macierze transformacji. W oparciu o wyznaczone macierze transformacji obliczona zostanie macierz transformacji z ostatniego układu współrzędnych do bazowego układu współrzędnych.
Proste zadanie kinematyki 1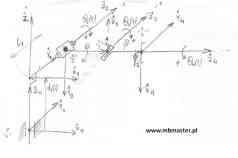
Rozwiązanie prostego zadania kinematyki dla manipulatora wyposażonego w trzy napędy obrotowe i jeden napęd przesuwny. W przykładzie wyznaczona zostanie tabelka parametrów zgodnie z notacją Denavita-Hartenberga. Następnie w oparciu o wyznaczone parametry z tabelki wyznaczone zostaną macierze transformacji pomiędzy kolejnymi układami współrzędnych związanych z robotem. Z rozważanym manipulatorem związane są cztery układy współrzędnych, wyznaczone zostaną więc cztery macierze transformacji. W oparciu o wyznaczone macierze transformacji obliczona zostanie macierz transformacji z ostatniego układu współrzędnych do bazowego układu współrzędnych → 40T.
Proste zadanie kinematyki 2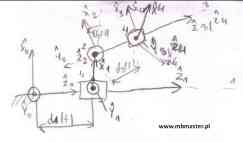
Rozwiązanie prostego zadania kinematyki dla manipulatora wyposażonego w dwa napędy obrotowe i dwa napędy przesuwne. W przykładzie wyznaczona zostanie tabelka parametrów zgodnie z notacją Denavita-Hartenberga. Następnie w oparciu o wyznaczone parametry z tabelki wyznaczone zostaną macierze transformacji pomiędzy kolejnymi układami współrzędnych związanych z robotem. Z rozważanym manipulatorem związane są cztery układy współrzędnych, wyznaczone zostaną więc cztery macierze transformacji. W oparciu o wyznaczone macierze transformacji obliczona zostanie macierz transformacji z ostatniego układu współrzędnych do bazowego układu współrzędnych → 40T.
Proste zadanie kinematyki 3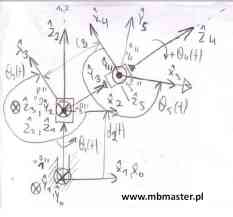
Rozwiązanie prostego zadania kinematyki dla manipulatora wyposażonego w cztery napędy obrotowe i jeden napęd przesuwny. W przykładzie wyznaczona zostanie tabelka parametrów zgodnie z notacją Denavita-Hartenberga. Następnie w oparciu o wyznaczone parametry z tabelki wyznaczone zostaną macierze transformacji pomiędzy kolejnymi układami współrzędnych związanych z robotem. Z rozważanym manipulatorem związanych jest pięć układów współrzędnych, wyznaczone zostanie więc pięć macierzy transformacji. W oparciu o wyznaczone macierze transformacji obliczona zostanie macierz transformacji z ostatniego układu współrzędnych do bazowego układu współrzędnych → 50T.
Proste zadanie kinematyki 4