Macierz rotacji opisuje transformację pomiędzy dwoma układami współrzędnych. W przedstawionym przykładzie są dwa układy kartezjańskie {A} i {B}. Wyznaczona zostanie macierz rotacji opisują transformację z układu {B} do układu {A}. Znajomość takiej macierzy pozwala na przetransformowanie współrzędnych dowolnego wektora z układu {B} do układu {A}.
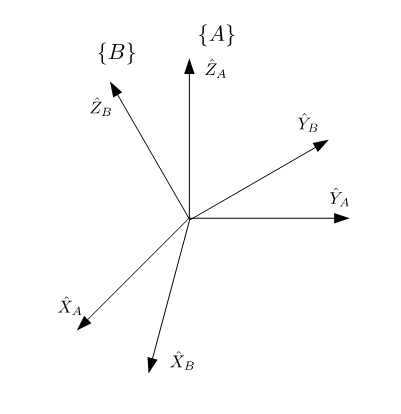
Wyrazy \hat X_{B}, \hat X_{A}, \hat Y_{B}, \hat Y_{A} , \hat Z_{B}, \hat Z_{A} są wersorami tj. wektorami jednostkowymi.
Kolejne wyrazy macierzy _{B}^{A}\bm{R} wyznaczane są w następujący sposób:
\hat X_{B} \cdot \hat X_{A} = |\hat X_{B}| \cdot |\hat X_{A}| \cos{\sphericalangle{(\hat X_{B},\hat X_{A})}}