Rozwiązane zadania i przykłady z teorii sterowania i przetwarzania sygnałów. Rozwiązanych jest szereg zadań dotyczących metody operatorowej. Metoda operatorowa jest szeroko stosowana w automatyce, ponieważ pozwala ona na przedstawienie równań różniczkowych w „wygodniejszej” postaci. W przykładach wyznaczane są modele matematyczne obiektów w postaci transmitancji operatorowej oraz równań stanu. Rozważane obiekty dynamiczne to zarówno układy mechaniczne i obwody elektryczne. Na stronie zamieszczone sa również kompaktowe notatki dotyczące: sterowania napędem pneumatycznym, sterowania napędem hydraulicznym oraz metod identyfikacji modeli matematycznych.
Wersja anglojęzyczna:
Control theory
Metoda operatorowa – zadania
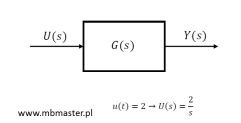
W teorii sterowania podczas analizy sygnałów i tworzenia modeli matematycznych badanych obiektów szeroko stosowana jest metoda operatorowa. Wygodnie jest przekształcić interesujące nas sygnały do postaci operatorowej a następnie wykonać dalsze obliczenia. Inaczej metoda operatorowa nazywana jest transformacją Laplace’a. Metoda operatorowa stosowana jest do rozwiązywania równań różniczkowych. Obiekty z którymi spotykamy się w automatyce bardzo często są opisane równaniami różniczkowymi. Podczas badania reakcji obiektów podawane są na ich wejścia różne wymuszenia. Podstawowym sygnałem wymuszającym jest funkcja jednykowa 1(t). Funkcję jedynkowa jest funckją skokową, często spotykana jest ona pod nazwą funkcji Heaviside’a lub skoku jednostkowego. W wyniku podania na wejście obiektu pewnego sygnału na jego wyjściu pojawia się odpowiedź w postaci sygnału wyjściowego.
Transmitancja operatorowa – zadania
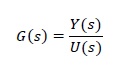

Transmitancja operatorowa jest jednym z rodzajów modeli matematycznych obiektów. Transmitancję operatorową G(S) definiujemy jako stosunek transformaty Laplace’a sygnału wyjściowego Y(s) do transformaty Laplace’a sygnału wejściowego U(s). Model matematyczny obiektu w postaci transmitancji operatorowej łączy w jednym równaniu zależność miedzy sygnałem wejściowym a sygnał wyjściowym. Znając transmitancję operatorową obiektu można wyznaczyć jego odpowiedź na zadane wymuszenie. Sygnałami wejściowymi i wyjściowymi mogą być różne wielkości fizyczne. W przypadku układów elektrycznych sygnałem wejściowym może być napięcie U a sygnałem wyjściowym prąd I. W układach mechanicznych sygnałem wejściowym może być siła F a sygnałem wyjściowym przesunięcie δx. Modelowany obiekt może być też hybrydą, czyli połączeniem układu mechanicznego i elektrycznego. W przypadku obiektu elektromechanicznego sygnałem wejściowym może być napięcie U a sygnałem wyjściowym moment M. Przykładem obiektu elektromechanicznego jest silnik indukcyjny. W rozwiązanych zadaniach zamieszczonych poniżej wyznaczana jest transmitancja operatorowa dla różnych obiektów elektrycznych i mechanicznych.
Transmitancja operatorowa – zadania
Zmienne stanu – zadania
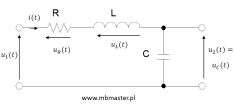
Zmienne stanu są jednym z sposobów tworzenia modeli matematycznych obiektów dynamicznych. Liczba zmiennych stanu danego układu jest równa liczbie magazynów energii. Przykładami magazynów energii dla układów elektrycznych są:
• kondensator C → gromadzi energię w polu elektrycznym
• cewka L → gromadzi energię w polu magnetycznym
Przykładami magazynów energii dla układów mechanicznych są:
• bryła o masie m[kg] w ruchu postępowym → energia kinetyczna w ruchu postępowym
• bryła o momencie bezwładności J[kg·m2 podczas ruchu obrotowego → energia kinetyczna w ruchu obrotowym
• sprężyna o sztywności k[N/m] → energia potencjalna zgromadzona w sprężynie
W oparciu o zmienne stanu tworzymy równania stanu. Równania stanu tworzą układ równań. Układ równań stanu zapisujemy z zastosowaniem rachunku macierzowego.

Podstawy teorii przetwarzania sygnałów
Zadania i przykłady z przetwarzania sygnałów
Każdy automatyk spotkał się pojęciem transmitancji operatorowej oraz równań stanu. Każdy układ ma liczbę zmiennych stanu równą liczbie magazynów energii. Przykładowymi magazynami energii są: masa, kondensator, cewka. Zamieszone są tu przykłady z wyznaczaniem transmitancji operatorowej oraz z zapisem w przestrzeni stanu dla tych samych układów. Dodatkowo na końcu rozważań dotyczących modelu matematycznego w postaci transmitancji operatorowej lub równań stanu jest podpowiedź jak je wykorzystać w programie MATLAB. Jak potężnym narzędziem dla inżyniera jest program MATLAB to nie trzeba chyba nikogo przekonywać.
Sterowanie napędem pneumatycznym
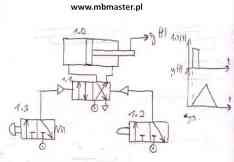
Automatyka to przede wszystkim regulacja(regulacja = sterowanie i kontrola). Bardzo często spotykamy problem sterowania napędami. Najpopularniejsze są w dzisiejszym przemyśle napędy elektryczne. Jednak możliwości napędowych jest więcej(wymienię tylko trzy, ale to nie wszystkie): napęd spalinowy, napęd hydrauliczny oraz napęd pneumatyczny. W zamieszczonym poniżej kompaktowym skrypcie z notatek jakie zrobiłem podczas moich studiów zamieszczone są informacje dotyczące pneumatyki i napędu pneumatycznego. W automatyce bardzo często spotykanym elementem wykonawczym są siłowniki pneumatyczne wraz z sprzężeniami zwrotnymi ich pozycji w postaci inicjatorów. Zasady działania i budowa podstawowych elementów używanych w pneumatyce takich jak: elektrozawory, zawory dławiąco-zwrotne, stacje przygotowania sprężonego powietrza, osuszacze, siłowniki pneumatyczne. Sprężone powietrze jest jednym z podstawowych nośników energii w automatyce. Pneumatyczne elementy wykonawcze są szeroko stosowane w układach automatycznej regulacji. Zaletą stosowania układów pneumatycznych jest ich iskrobezpieczność. Opisane są podstawowe właściwości sprężonego powietrza oraz elementów wykonawczych zasilanych sprężonym powietrzem. W notatkach wyjaśnione jest działanie układów logicznych zrealizowanych za pomocą urządzeń pneumatycznych. Skrypt zawiera także przykłady podstawowych konstrukcji stosowanych w pneumatyce.
Pneumatyka i sterowanie napędem pneumatycznym
Sterowanie napędem hydraulicznym
Zasady działania i budowa podstawowych elementów używanych w hydraulice takich jak pompy hydrauliczne, silniki hydrauliczne, akumulatory hydrauliczne, zawory hydrauliczne. W notkach opisana jest budowa pompy zębatej, pompy łopatkowej oraz pompy zębatej o zazębieniu wewnętrznym. W opracowaniu zawarte są podstawowe informacje dotyczące obiegu hydrostatycznego, charakterystyk pracy pomp wyporowych. W notatkach opisane są także podstawowe układy stosowane w hydraulice takie jak układ stałego momentu maksymalnego, układ stałej mocy maksymalnej oraz układ stałej siły maksymalnej.
Sterowanie napędem hydraulicznym
Metody identyfikacji modeli matematycznych
Dla niektórych obiektów automatycznej regulacji jest możliwość stworzenia modelu matematycznego wprost. Modele matematyczne prostych obiektów wyznaczamy z zastosowaniem znanych nam praw fizyki stosowanych w mechanice, elektrotechnice oraz innych dziedzinach ścisłych. W ogólności jednak wyznaczenie modelu matematycznego obiektu regulacji jest zadaniem bardziej złożonym. Wyznaczanie modelu matematycznego skomplikowanego procesu automatyki z zastosowaniem znanych nam teorii jest zadaniem bardzo trudnym i czasochłonnym. W praktyce inżynierskiej bardzo często tworzymy model danego obiektu poprzez wykonanie eksperymentu. Na podstawie pomiarów uzyskanych w doświadczeniu i metod matematycznych tworzymy model matematyczny obiektu. Metody matematyczne o których mowa to:
• Interpolacja paraboliczna metodą Lagrange’a
• Aproksymacja funkcji dwóch zmiennych metodą różnic podwójnych
• Metoda najmniejszych kwadratów błędów
• Metoda analizy regresji
• Metoda analizy czynnikowej
Model matematyczny musi jak najlepiej odzwierciedlać obiekt. Posiadanie dobrego modelu matematycznego pozwala na badanie właściwości obiektu w sposób teoretyczny bez uciekania się do często kosztownych doświadczeń.