Wzór ogólny na wartość skuteczną (RMS – root mean square)
F_{RMS} = \sqrt{\frac{1}{T}\int_{0}^{T}{f^{2}(t)\cdot dt}}
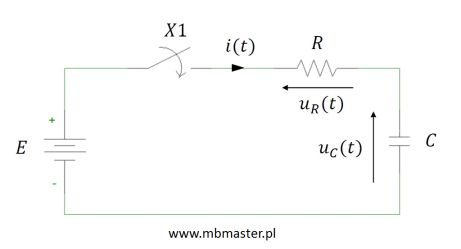
Interpretacja tej wielkości na podstawie wartości skutecznej prądu.
u(t) = R \cdot i(t)
W = \int{p \cdot dt}
W = \int{u \cdot i \cdot dt}
W = R\cdot \int{ i^{2} \cdot dt}
gdzie:
W – praca
p – moc chwilowa
p = u \cdot i
u – napięcie chwilowe
i – prąd chwilowy
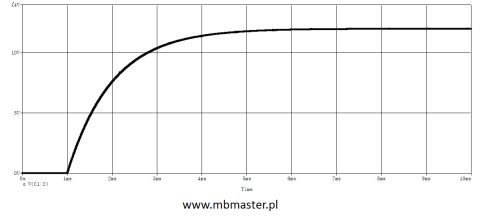
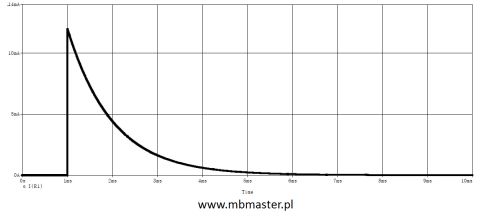
Jeżeli przebieg jest okresowy to
W_{T} = R\cdot \int_{0}^{T}{ i^{2} \cdot dt}Wartość skuteczna jest to prąd stały który wydzieli tyle samo ciepła.
R\cdot \int_{0}^{T}{ i^{2} \cdot dt} = R \cdot I^{2} \cdot T
Dzieląc powyższe równanie obustronnie przez R
\int_{0}^{T}{ i^{2} \cdot dt} = I^{2} \cdot T
Następnie zamieniając strony tak aby wyznaczyć prąd stały I
I^{2} \cdot T = \int_{0}^{T}{ i^{2} \cdot dt}
Finalnie uzyskuje się
Wartość skuteczna prądu
I_{RMS} = \sqrt{\frac{1}{T}\cdot \int_{0}^{T}{ i^{2} \cdot dt}}Wartość skuteczna napięcia
U_{RMS} = \sqrt{\frac{1}{T}\cdot \int_{0}^{T}{ u^{2} \cdot dt}}