Rezystancja jest jedną z pierwszych wielkości jaką poznajemy w elektrotechnice. Prawo Ohma wiąże za pomocą rezystancji w jednym równaniu prąd I i napięcie U.
Prawo Ohma → I=U/R lub U=R·I
gdzie
• R – rezystancja [Ω]
• U – napięcie elektryczne [V]
• I – prąd elektryczny [A]
Rezystancja jest zależna od geometrii przewodnika. Przewodnik musi mieć jednakowy przekrój poprzeczny na całej długości. Prąd elektryczny przepływa w kierunku prostopadłym do przekroju.
R=ρ·l/S
gdzie
• ρ – rezystywność właściwa [Ω/m]
• l – długość przewodnika [m]
• S – pole przekroju poprzecznego [m2]
Podczas wyznaczania rezystancji zastępczej bardzo przydatna jest relacja pomiędzy rezystancją a konduktancją.
G=1/R
R=1/G
Jednostką konduktancji jest Siemens [S].
W ogólności rozróżniamy dwa elementarne sposoby łączenia rezystancji.
• połączenie szeregowe rezystorów → przez rezystory przepływa ten sam prąd, rezystancja zastępcza jest równa sumie algebraicznej rezystancji składowych.
R=R1+R2+…+Rn
• połączenie równoległe rezystorów → do zacisków rezystorów jest przyłożone to samo napięcie, wówczas odwrotność rezystancji zastępczej jest równa sumie algebraicznej odwrotności rezystancji składowych
1/R=1/R1+1/R2+…+1/Rn
Podczas wyznaczania rezystancji połączenia równoległego rezystorów wygodnie jest skorzystać z zależności pomiędzy rezystancją a konduktancją.
G=G1+G2+…+Gn
Bardzo często podczas analizowania obwodów elektrycznych zarówno prądu stałego jak i pradu zmiennego traktujemy rezystancję jako stałą. W ogólności rezystancja zależy od temperatury R=R(T).
R(T)=R0·(1+α·(T-T0)
W równaniu powyżej przedstawiliśmy rezystancję przewodnika jako liniową zależność od temperatury. W rzeczywistości nie musi być tak kolorowo. W zależności od materiału i od zakresu temperatur rezystancja może zależeć liniowo od temperatury, bądź może być opisana równaniem wielomianowym. Przykładem spełnienia równania R(T) przedstawionego powyżej jest charakterystyka parametrycznego czujnika temperatury Pt100 dla zakresu temperatury 0[°C]-100[°C].
Rezystancja zależy również od częstotliwości R=R(f) przepływającego prądu. W przypadku prądu stałego którego częstotliwość f=0[Hz] zjawisko to nie występuje. W przypadku prądu przemiennego rezystancja wzrasta wraz z wzrostem częstotliwości f, związane jest to z zjawiskiem naskórkowości(en. skin effect).
W przypadku przewodników ich rezystancja wzrasta wraz z wzrostem temperatury. Przewodniki nie są jedynym rodzajem materii z jakim się spotykamy. Innym przykładem są półprzewodniki. W przypadku półprzewodników ich rezystancja może zarówno rosnąć jak i maleć wraz ze wzrostem temperatury. W półprzewodnikach za rezystancję odpowiadają dwa mechanizmy. Pierwszy mechanizm jest związany z geometrią półprzewodnika a drugi z nośnikami ładunków w półprzewodniku. W wyniku wzrostu temperatury w półprzewodnikach uwalnia się więcej nośników ładunków. W zależności który z mechanizmów w półprzewodniku ma przewagę może w efekcie powodować wzrost lub zmniejszenie się jego rezystancji wraz z wzrostem temperatury. Praktycznym przykładem są półprzewodnikowe czujniki temperatury:
• czujnik PTC (en. positive temperature coefficient) → rezystancja wzrasta wraz z wzrostem temperatury
• czujnik NTC (en. negative temperature coefficient) → rezystancja maleje wraz z wzrostem temperatury
Rezystory połączone szeregowo
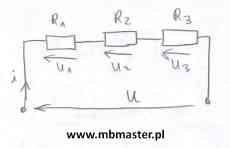
Obwód elektryczny zbudowany jest z trzech rezystorów połączonych szeregowo. Każdy rezystor traktowany jest jako element o parametrach skupionych. Dla tak skonstruowanego obwodu elektrycznego wyprowadzona zostanie zależność na rezystancję zastępczą widzianą od strony źródła zasilania obwodu. Elementy w obwodzie połączone są szeregowo. Cechą połączenia szeregowego jest ten sam prąd I, który płynie przez obwód. Do wyprowadzenia wzoru na rezystancję zastępczą zastosowane zostanie prawo Ohma oraz napięciowe prawo Kirchhoffa.
Rezystory połączone równolegle
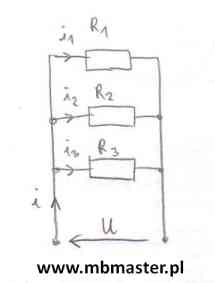
Obwód elektryczny zbudowany jest z trzech rezystorów połączonych równolegle. Każdy rezystor traktowany jest jako element o parametrach skupionych. Dla tak skonstruowanego obwodu elektrycznego wyprowadzona zostanie zależność na rezystancję zastępczą widzianą od strony źródła zasilania obwodu. Elementy w obwodzie połączone są równoległe. Cechą połączenia szeregowego jest to samo napięcie U między zaciskami elementów. Do wyprowadzenia wzoru na rezystancję zastępczą zastosowane zostanie prawo Ohma oraz prądowe prawo Kirchhoffa.
Rezystory połączone równolegle
Rezystancja – zadanie 1
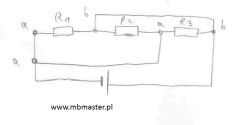
Rozwiązany przykład z wyznaczaniem rezystancji zastępczej obwodu elektrycznego. W rozważanym zadaniu korzystamy z zależności pomiędzy konduktancją a rezystancją R=1/G lub równoważnie G=1/R. Jednostką fizyczną opisującą rezystancję jest Ohm [Ω]. Konduktancja również posiada jednostkę a jest nią Siemens [S]. Rezystancja połączeń szeregowych rezystorów została wyliczona z wzoru na rezystancję zastępczą rezystorów połączonych w szereg. Rezystancja rezystorów połączonych równolegle została wyznaczona z użyciem zależności na konduktancję.
Rezystancja wypadkowa przykład
Rezystancja – zadanie 2
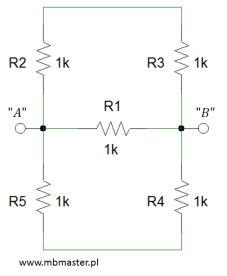
Wyznaczanie rezystancji zastępczej układu ośmiu rezystorów. Rezystory w układzie połączone w mieszany sposób, raz są połączone równolegle a raz są połączone szeregowo. W celu wyznaczenia rezystancji zastępczej konieczna jest znajomość podstawowej zasady przepływu prądu elektrycznego → aby prąd elektryczny przepływał pomiędzy dwoma dowolnymi punktami to pomiędzy tymi punktami musi występować różnica potencjałów. Wszystkie rezystory mają taką samą wartość rezystancji równą 1[kΩ].
Rezystancja – zadanie 3
Wyznaczanie rezystancji zastępczej układu pięciu rezystorów. Rezystory są połączone w obwodzie równolegle oraz szeregowo. Podczas wyliczania rezystancji zastępczej obwodu wykorzystana zostanie relacja pomiędzy konduktancją a rezystancją → G=1/R.
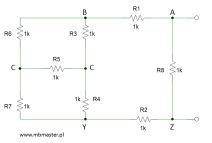
Rezystancja – zadanie 4
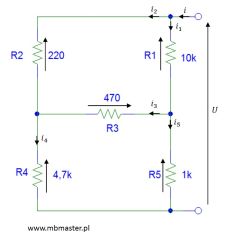
Wyznaczanie rezystancji zastępczej układu pięciu rezystorów połączonych w kształt litery H. Do połączonego w ten sposób układu rezystorów nie ma możliwości zastosowania zasad połączeń szeregowych i połączeń równoległych rezystorów. Rezystancja zastępcza tego specyficznego połączenia rezystorów zostanie wyznaczona zastosowaniem praw Kirchhoffa dla obwodów elektrycznych i prawa Ohma. W efekcie końcowym dla rozważanego obwodu elektrycznego zostanie otrzymana rezystancja zastępcza w postaci dość sporego ułamka. Dla obwodu tego przeprowadzona została również symulacja w programie Pspice wraz z równoczesnymi wyliczeniami w arkuszu kalkulacyjnym programu Excel.
Rezystancja – zadanie 5
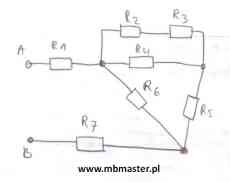
Wyznaczanie rezystancji zastępczej układu siedmiu rezystorów. Rezystory połączone są w sposób mieszany, raz są połączone szeregowo a raz równolegle. W zadaniu wykorzystana zostanie relacja pomiędzy rezystancją a konduktancją → G=1/R. Relacja ta będzie wykorzystana do wygodnego obliczania połączeń równoległych rezystorów. W zadaniu wyznaczona zostanie rezystancja obwodu „widziana” od strony zacisków zasilających A i B.