Archiwum kategorii: Dynamika

Równania Lagrange’a dla układu mechanicznego

Dynamika, Mechanika,

Dynamika trójmasowego układu mechanicznego w ruchu obrotowym. W rozważanym przykładzie zastosowane zostanie zapis energii w formie wariacyjnej tj. innymi słowy w postaci równań Eulera-Lagrange’a pierwszego rodzaju.

Trójmasowy układ mechaniczny

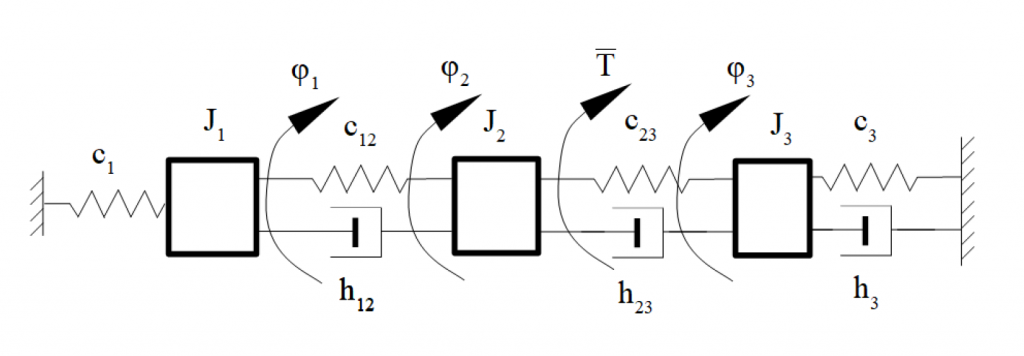
Ogólna postać równań Lagrange’a
L = E_k - V

Równania Lagrange’a pierwszego rodzaju:

\frac{d}{dt}\frac{\partial{L}}{\partial{{\dot{q_i}}}} - \frac{\partial{L}}{\partial{q_i}} + \frac{\partial{D}}{\partial{{\dot{q_i}}}} = \sum_{k}{Q_{k}}

Znaczenie symboli:

L \rightarrow Lagrangian E_k \rightarrow energia \,kinetyczna V \rightarrow energia \,potencjalna D \rightarrow \,dyssypacja \,energii q_i \rightarrow zmienna \,o \,indeksie \,i \dot{ q_i} \rightarrow pierwsza \,pochodna \,po \,czasie

Zmienne w rozważanym układzie mechanicznym:

q_1 = \varphi_1, \dot q_1 =\dot \varphi_1 q_2 = \varphi_2, \dot q_2 =\dot \varphi_2 q_3 = \varphi_3, \dot q_3 =\dot \varphi_3

Energia kinetyczna:

E_k = \frac{1}{2}\cdot J_1 \cdot \dot{\varphi_1}^2 + \frac{1}{2}\cdot J_2 \cdot \dot{\varphi_2}^2 + \frac{1}{2}\cdot J_3 \cdot \dot{\varphi_3}^2

Energia potencjalna:

V = \frac{1}{2}\cdot c_1 \cdot \varphi_{1}^2 + \frac{1}{2}\cdot c_{12} \cdot (\varphi_{2} - \varphi_{1})^2 + \frac{1}{2}\cdot c_{23} \cdot (\varphi_{2} - \varphi_{3})^2 + \frac{1}{2}\cdot c_3 \cdot \varphi_{3}^2

Dyssypacja energii:

D = \frac{1}{2}\cdot h_{12} \cdot (\dot\varphi_{2} - \dot\varphi_{1})^2 + \frac{1}{2}\cdot h_{23} \cdot (\dot\varphi_{2} - \dot\varphi_{3})^2 + \frac{1}{2}\cdot h_3 \cdot \dot\varphi_{3}^2

Równania dla zmiennej q1:

J_1 \cdot \ddot \varphi_1 - (-c_1 \cdot \varphi_1 - c_{12} \cdot (\varphi_2 - \varphi_1) \cdot (-1)) + (h_{12}\cdot (\dot \varphi_2 - \dot \varphi_1)\cdot (-1)) = 0
J_1 \cdot \ddot \varphi_1 + c_1 \cdot \varphi_1 - c_{12} \cdot (\varphi_2 - \varphi_1) - h_{12}\cdot (\dot \varphi_2 - \dot \varphi_1) = 0
J_1 \cdot \ddot \varphi_1 = - c_1 \cdot \varphi_1 + c_{12} \cdot (\varphi_2 - \varphi_1) + h_{12}\cdot (\dot \varphi_2 - \dot \varphi_1)

Równania dla zmiennej q2:

J_2 \cdot \ddot \varphi_2 - (-c_{12}\cdot (\varphi_2 - \varphi_1) -c_{23}\cdot (\varphi_2 - \varphi_3)) + (h_{12}\cdot (\dot\varphi_2 - \dot\varphi_1) + h_{23}\cdot (\dot\varphi_2 - \dot\varphi_3)) = T
J_2 \cdot \ddot \varphi_2 + c_{12}\cdot (\varphi_2 - \varphi_1) + c_{23}\cdot (\varphi_2 - \varphi_3) + h_{12}\cdot (\dot\varphi_2 - \dot\varphi_1) + h_{23}\cdot (\dot\varphi_2 - \dot\varphi_3) = T
J_2 \cdot \ddot \varphi_2 = - c_{12}\cdot (\varphi_2 - \varphi_1) - c_{23}\cdot (\varphi_2 - \varphi_3) - h_{12}\cdot (\dot\varphi_2 - \dot\varphi_1) - h_{23}\cdot (\dot\varphi_2 - \dot\varphi_3) + T

Równania dla zmiennej q3:

J_3 \cdot \ddot \varphi_3 - (-c_{23}\cdot (\varphi_2 - \varphi_3)\cdot(-1) -c_{3}\cdot \varphi_3) + (h_{23}\cdot (\dot\varphi_2 - \dot\varphi_3)\cdot(-1) + h_{3}\cdot \dot\varphi_3) = 0
J_3 \cdot \ddot \varphi_3 - c_{23}\cdot (\varphi_2 - \varphi_3) + c_{3}\cdot \varphi_3 - h_{23}\cdot (\dot\varphi_2 - \dot\varphi_3) + h_{3}\cdot \dot\varphi_3 = 0
J_3 \cdot \ddot \varphi_3 = c_{23}\cdot (\varphi_2 - \varphi_3) - c_{3}\cdot \varphi_3 + h_{23}\cdot (\dot\varphi_2 - \dot\varphi_3) - h_{3}\cdot \dot\varphi_3


Dynamika w ruchu obrotowym

Dynamika, Mechanika,

W przykładzie rozpatrzony zostanie układ mechaniczny o trzech stopniach swobody. W jednym miejscu układu przyłożony jest zewnętrzny moment T. Rozpatrywany układ posiada w swojej strukturze elementy sprężyste i tłumiące.

Układ mechaniczny o trzech stopniach swobody

Równanie dla pierwszego stopnia swobody:

J_{1}\cdot \ddot{\varphi_1} = -c_1\cdot\varphi_1 + c_{12}\cdot(\varphi_2 - \varphi_1) + h_{12}\cdot(\dot{\varphi_2} - \dot{\varphi_1})

Równanie dla drugiego stopnia swobody

J_{2}\cdot \ddot{\varphi_2} = -c_{12}\cdot(\varphi_2 - \varphi_1) - h_{12}\cdot(\dot{\varphi_2} - \dot{\varphi_1}) - c_{23}\cdot(\varphi_2 - \varphi_3) - h_{23}\cdot(\dot{\varphi_2} - \dot{\varphi_3}) + T

Równanie dla trzeciegostopnia swobody

J_{3}\cdot \ddot{\varphi_3} = -c_3\cdot\varphi_3 - h_3\cdot\dot\varphi_3+ c_{23}\cdot(\varphi_2 - \varphi_3) + h_{23}\cdot(\dot{\varphi_2} - \dot{\varphi_3})

Drgania masy na sprężynie

Dynamika, Mechanika, ,

Wyznaczanie równania ruchu dla masy drgającej na sprężynie. W rozważanym układzie kula o masie m [kg] jest przytwierdzona do sufitu za pomocą sprężyny o sztywności k [\frac{N}{m}].

Masa drgająca

Równanie ruchu dla rozważanego układu jest postaci:

m \cdot \vec{a} = -k\cdot \vec{x}

Rozważane równanie ruchu jest równaniem różniczkowym pierwszego rzędu o zmiennych rozdzielonych.

m \cdot \frac{d^2x}{dt^2} = -k\cdot x

Stosując zapis Newton-a tj. oznaczając kolejne pochodne względem czasu poprzez kropki nad różniczkowaną zmienną, równanie ruchu ma postać:

m \cdot \ddot x = -k\cdot x

Oscylator harmoniczny prosty

Opór ruchu – tarcie

Dynamika, Mechanika, Statyka, , ,

Tarcie toczne - zadanie 2.

Zjawisko tarcia jest jednym z podstawowych oporów ruchu z jakim spotykamy się w mechanice. Tarcie jest oporem materii, która przeciwdziała ruchowi ciała umieszczonego w niej. Opór powietrza jest przykładem oporu materii. W mechanice najczęściej spotykamy się z dwoma rodzajami tarcia:
• tarciem przesuwnym (siła tarcia powstaje w wyniku przesuwania się po sobie powierzchni lub próby przesunięcia bez wprowadzenia w ruch)
• tarciem tocznym (opór podczas toczenia ciał)
Gdy tarcie nie występowało to na mocy pierwszej zasady dynamika Newtona ciało raz rozpędzone poruszałoby się ruchem jednostajnym w nieskończoność, gdyby na ciało działała niezrównoważona siła to na mocy drugiej zasady dynamiki Newtona ciało rozpędzałoby się w nieskończoność. Oczywiście jak wiemy z doświadczeń oba hipotetyczne przypadki nie występują. Pierwszy przypadek jest niemożliwy z uwagi na występowanie oporu materii, a drugi przypadek z powodu oporu materii oraz ograniczeń związanych Szczególną Teorią Względności Alberta Einsteina (żadne ciało posiadające masę spoczynkową większą od zera, nie może osiągnąć prędkości większej od prędkości światła c w próżni).

Mechanika tarcie – zadania

Przyśpieszenie liniowe rozwijającego się wałka

Dynamika, Mechanika, ,

Mechanika dynamika - wyznaczanie przyśpieszenia rozwijającego się wałka.

Wyznaczanie przyśpieszenia liniowego z jakim porusza się wałek. Wałek przywiązany jest na nieważkiej nici do sufitu. Wałek posiada masę m, a jego podstawa ma promień r. Układ znajduje się pod wpływem ziemskiego pola grawitacyjnego. Rozwijący wałek porusza się ruchem płaskim pionowo w dół. Ruch płaski to połączenie ruchu liniowego i ruchu obrotowego.

Dynamika – przyśpieszenie rozwijającego się wałka