Polecam rozwiązane zadania i przykłady z podstaw robotyki. Znaleźć tutaj można rozwiązane zadania z prostym zadaniem kinematyki i odwrotnym zadaniem kinematyki. Jak ktoś ma trudności z kątami Eulera to również znajdzie przykład. Dla leniwych studentów jest tu cały projekt z dynamiki robotów, może on być bardzo pomocny podczas realizacji własnego.
Robotyka proste zadanie kinematyki
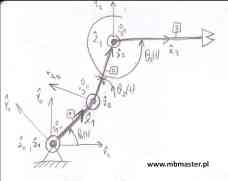
Proste zadanie kinematyki polega wyznaczaniu wektora pozycji danego punktu w układzie kartezjańskim, którym najczęściej jest układ bazowy. W prostym zadaniu kinematyki znane są kąty ugięcia Θi oraz przesunięcia danych członów di. W oparciu o znajomość tych wielkości wyznaczamy współrzędne kartezjańskie wektora pozycji w danym układzie współrzędnych. Proste zadanie kinematyki polega na przejściu z przestrzeni zmiennych przegubowych do przestrzeni kartezjańskiej. W skrócie proste zadanie kinematyki można symbolicznie jako:
{Θi,di} → {Xi,Yi,Zi}
Rozwiązanie kinematyki prostej manipulatora(robota) polega na zapisaniu tabelki parametrów zgodnie z notacją Denavita-Hartenberga. Następnie w oparciu o uzyskane parametry i postać ogólną macierzy transformacji ii-1T z układu „i” do „i-1” tworzy się macierze transformacji pomiędzy kolejnymi układami współrzędnych.
Wersja anglojęzyczna:
Robotics
Robotyka odwrotne zadanie kinematyki

Kinematyka odwrotna robota jest transformacją pozwalającą na wyliczenie na podstawie współrzędnych z kartezjańskiego układu współrzędnych (najczęściej układu bazowego lub inaczej układu zerowego) kąty ugięć lub przesunięcia zmiennych przegubowych. W skórcie odwrotne zadanie kinematyki można zapisać jako:
{Xi,Yi,Zi} → {Θi,di}
Znane są nam więc współrzędne kartezjańskie, na ich podstawie chcemy uzyskać zmienne kąty ugięć (w przypadku napędu obrotowego) lub przesunięcia (w przypadku napędu liniowego). Kinematyka odwrotna jest zagadnieniem zdecydowanie bardziej złożonym od kinematyki prostej. Przede wszystkim kinematyka prosta robota jest częścią procesu wyznaczania jego kinematyki odwrotnej. W kinematyce odwrotnej porównujemy między sobą dwie macierze transformacji. Pierwszą macierzą transformacji jest macierz uzyskana jako wynik kinematyki prostej. Drugą macierzą jest zadana macierz transformacji. Macierz zadana jest przejściem od pierwszego do ostatniego układu współrzędnych poprzez wektor przesunięcia oraz rotację.
Odwrotne zadanie kinematyki kompletny projekt
Robotyka kąty Eulera przykład
Macierz rotacji opisuje rotację pomiędzy jednym układem współrzędnych a drugim układem współrzędnych w ogólności macierz rotacji przedstawiająca transformację współrzędnych z układu {B} do układu {A} jest postaci:

Jak widać na rysunku powyżej macierz rotacji jest macierzą iloczynów skalarnych wersorów kolejnych osi układów współrzędnych {A} i {B}.
Kąty Eulera opisują dowolną rotację pomiędzy układami współrzędnych kartezjańskich. W ogólności każdą rotację można przedstawić jak złożenie trzech obrótów pomiędzy układami współrzędnych. Każdy z obrotów składowych jest rotacją wokół jednej z osi. W rozważanych tutaj przykładach obroty bedą następować kolejno wokół osi Z–Y–X. Tok postępowania podczas rotacji jest następujący
• Pierwszy obrót następuje wokół osi ZA układu wejściowego i odbywa sie w płaszczyźnie XAYA o kąt ψ, w efekcie powstaje układ {B’}, osie ZA i ZB’ pokrywają się.
• Drugi obrót następuje wokół osi YB’ układu {B’} i odbywa sie w płaszczyźnie XB’ZB’ o kąt θ, w efekcie powstaje układ {B”}, osie YB” i YB’ pokrywają się.
• Trzeci obrót następuje wokół osi XB” układu {B”} i odbywa sie w płaszczyźnie YB”ZB” o kąt φ, w efekcie powstaje układ wyjściowy {B}, osie XB i XB’ pokrywają się.
W ogólności macierz z układu {B} do {A} jest równa iloczynowi trzech macierzy.
Kąty Eulera i macierze rotacji – zadania
Dynamika robotów kompletny projekt
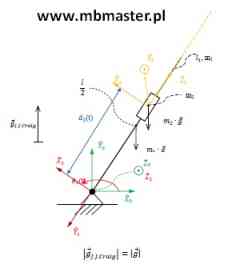
Poprzez rozwiązanie kinematyki prostej i kinematyki odwrotnej robota otrzymuje się macierze transformacji pozwalające na przeliczanie pozycji pomiędzy układami współrzędnych. Aby robot mógł osiągnąć daną pozycję musi się do niej przemieścić. Każdy przegub robota posiada napęd, do którego musi być dostarczona odpowiednia moc aby możliwe było jego poruszanie się z zdanymi prędkościami i przyśpieszeniami. Gdy robot znajduje się w stanie spoczynku jego serwonapędy obciążone są tylko statycznie, związane jest to z masą poszczególnych elementów. W stanie spoczynku napędy robota w zależności od jego konfiguracji mogą przenosić część obciążenia statycznego ponieważ pozostała część obciążenia statycznego będzie przenoszona przez konstrukcję manipulatora. Oczywiście robot jest wyposażony w serwonapędy, których częścią składową jest hamulec elektromagnetyczny. W stanie spoczynku manipulatora napędy nie są zasilane ponieważ przeguby utrzymywane są w równowadze poprzez hamulce.