Równania różniczkowe niekoniecznie muszą być rozwiązywane metodą klasyczną. Bardzo często stosowną metodą do rozwiązywania równań różniczkowych jest rachunek operatorowy, nazywany również często transformatą Laplace’a. Korzystając z transformacji Laplace’a do rozwiązania równania różniczkowego, otrzymujemy mówiąc z dużym uproszczeniem do rozwiązania równanie algebraiczne. Modele matematyczne układy dynamicznych bardzo często tworzone są z wykorzystaniem transformaty Laplace’a.
Podstawowe transformaty Laplace’a – wzory

Wzory na transformaty Laplace’a podstawowych funkcji. Rozwiązując równania różniczkowe metodą operatorową niezbędna jest znajomość podstawowych transformat Laplace’a.
Podstawowe transformaty Laplace’a
transformata Laplace’a – zadanie 1
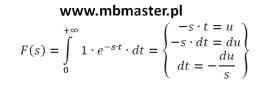
Wyznaczanie transformaty Laplace’a funkcji f(t)=1(t) → f(t)=1. Rozważana funkcja f(t) jest stała. Transformata Laplace’a tej funkcji zostanie wyznaczona z definicji.
Transformata Laplace’a zadanie 1
transformata Laplace’a – zadanie 2
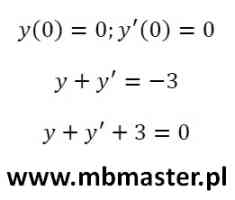
Rozwiązanie równania różniczkowego metodą operatorową. Równanie różniczkowe jest postaci y’+y=-3. Równanie różniczkowe zostanie przetransformowane do postaci operatorowej. Postać operatorowa równania zostanie rozbita na ułamki proste. W zadaniu wyznaczone zostaną współczynniki ułamków prostych oraz oryginały transformat funkcji przedstawionych poprzez ułamki.
Transformata Laplace’a zadanie 2
transformata Laplace’a – przykład 0
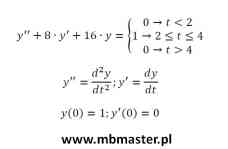
Rozwiązanie równania różniczkowego metodą operatorową. Równanie różniczkowe jest postaci y”(t)+8·y'(t)+16·y(t)={ 0 dla t<2; 1 dla 1≤t≤4; 0 dla t>4}. W trakcie wyznaczania transformaty Laplace’a równania różniczkowe trzeba wziąć pod uwagę również warunki początkowe y'(0)=0 oraz y(0)=1. W przykładzie zastosowane będzie twierdzenie o transformacie Laplace’a pochodnej funkcji. Wykorzystane zostaną również wzory na transformaty Laplace’a podstawowych funkcji. Współczynniki przy transformatach składowych zostaną wyznaczone z zastosowaniem metody rozbicia na ułamki proste.
Transformata Laplace’a przykład 0
transformata Laplace’a – przykład 1
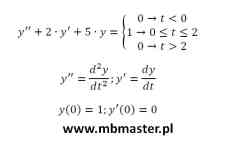
Rozwiązanie równania różniczkowego metodą operatorową. Równanie różniczkowe jest postaci y”(t)+2·y'(t)+5·y(t)={ 0 dla t<0; 1 dla 0≤t≤2; 0 dla t>2}. W trakcie wyznaczania transformaty Laplace’a równania różniczkowe trzeba wziąć pod uwagę również warunki początkowe y'(0)=0 oraz y(0)=1. W przykładzie zastosowane będzie twierdzenie o transformacie Laplace’a pochodnej funkcji. Wykorzystane zostaną również wzory na transformaty Laplace’a podstawowych funkcji. Współczynniki przy transformatach składowych zostaną wyznaczone z zastosowaniem metody rozbicia na ułamki proste.
Transformata Laplace’a przykład 1
transformata Laplace’a – przykład 2
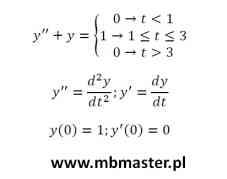
Rozwiązanie równania różniczkowego metodą operatorową. Równanie różniczkowe jest postaci y”(t)+y(t)={ 0 dla t<1; 1 dla 1≤t≤3; 0 dla t>3}. W trakcie wyznaczania transformaty Laplace’a równania różniczkowe trzeba wziąć pod uwagę również warunki początkowe y'(0)=0 oraz y(0)=1. W przykładzie zastosowane będzie twierdzenie o transformacie Laplace’a pochodnej funkcji. Wykorzystane zostaną również wzory na transformaty Laplace’a podstawowych funkcji. Współczynniki przy transformatach składowych zostaną wyznaczone z zastosowaniem metody rozbicia na ułamki proste
Transformata Laplace’a przykład 2
transformata Laplace’a – przykład 3
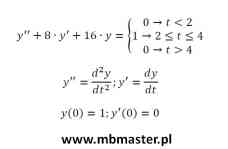
Rozwiązanie równania różniczkowego metodą operatorową. Równanie różniczkowe jest postaci y”(t)+8·y'(t)+16·y(t)={ 0 dla t<2; 1 dla 1≤t≤4; 0 dla t>4}. W trakcie wyznaczania transformaty Laplace’a równania różniczkowe trzeba wziąć pod uwagę również warunki początkowe y'(0)=0 oraz y(0)=1. W przykładzie zastosowane będzie twierdzenie o transformacie Laplace’a pochodnej funkcji. Wykorzystane zostaną również wzory na transformaty Laplace’a podstawowych funkcji. Współczynniki przy transformatach składowych zostaną wyznaczone z zastosowaniem metody rozbicia na ułamki proste