Statyka jest działem mechaniki. Podstawowym założeniem statyki jest jest brak ruchu w rozważanych przykładach. W statyce opierając się na równaniach rownowagi wyznaczamy siły rekacji działających na dane ciało. Często obliczamy również maksymalną siłę jaką można zadziałać na ciało nie powodując jego ruchu, czyli taką pod wpływem której dane ciało pozostanie w spoczynku a siły reakcji zrównoważą siłę wymuszającą. Biegła znajomość statyki jest niezbędna do dalszej nauki różnych dziedzin mechaniki jaką jest między innymi wytrzymałość materiałów. Podczas rozwiązywania zagadnienia przypisujemy do niego najczęściej kartezjański układ współrzędnych. W ogólnym przypadku aby ciało pozostawało w równowadze(spoczynku) spełnionych musi być sześć warunków:
⋅ Suma sił działających w kierunku osi X jest równa zero: ΣFix=0
⋅ Suma sił działających w kierunku osi Y jest równa zero: ΣFiy=0
⋅ Suma sił działających w kierunku osi Z jest równa zero: ΣFiz=0
⋅ Suma momentów sił działających wokół osi X jest równa zero: ΣTix=0
⋅ Suma momentów sił działających wokół osi Y jest równa zero: ΣTiy=0
⋅ Suma momentów sił działających wokół osi Z jest równa zero: ΣTiz=0
Wersja anglojęzyczna:
Statics
Mechanika statyka – zadanie 1
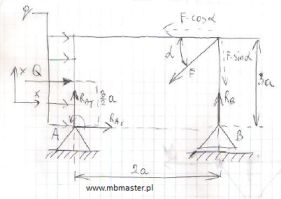
Mechanika statyka – płaski dowolny układ sił. Wyznaczanie równań równowagi dla ramy podpartej na dwóch podporach. Rama znajduje się wpływem obciążenia ciągłego i siły zewnętrznej.
Mechanika statyka – zadanie 2

Drut towrzący kształ litery C znajduje się wpływem obciążenia ciągłego i siły zewnętrznej. Jeden z końców konstrukcji podparty jest na podporze ruchomej. Drugi koniec podparty jest na podporze stałej.
Mechanika statyka – zadanie 3
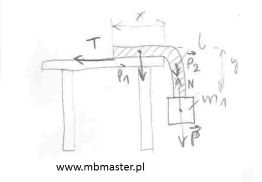
Mechanika statyka – przykład z tarciem sznura po blacie stołu, równania równowagi statycznej sił.
Mechanika statyka – zadanie 4
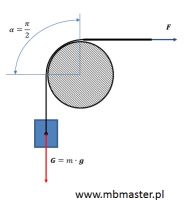
Prosty przykład z tarciem cięgien. Wzór na siły tarcia cięgien.
Mechanika statyka – zadanie 5
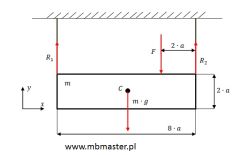
Wyznaczanie równań równowagi i sił reakcji dla belki przymocowanej do sufitu za pomocą sznurków. Na belkę działa dodatkowo siła zewnętrzna F.
Mechanika statyka – zadanie 6
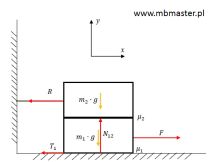
Klocki posiadające różne masy leżą na podłożu. Klocki ułożone są jeden na drugim. Górny klocek przymocowany jest sznurkiem do ściany. Na dolny klocek działa siła zewnętrzna F. Pomiędzy klockami występuje tarcie ślizgowe o współczynniku μ2. Pomiędzy dolnym klockiem a podłożem występuje tarcie ślizgowe o współczynniku μ1. Wyznaczanie równań równowagi dla układu.
Mechanika statyka – zadanie 7
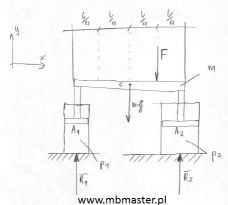
Belka o masie m[kg] i długości l[m] podparta jest na dwóch siłownikach pneumatycznych. Siłowniki pneumatyczne umieszczone są na końcach belki. Każdy z siłowników posiada taki sam skok. Siłownik mają różne średnice cylindrów. Na belkę działa dodatkowo siła wymuszająca umieszczona w ćwierć długości belki od jednego z końców. W zadaniu wyznaczone są równania równowagi statycznej oraz ciśnienia powietrza jakie muszą być wewnątrz siłowników aby układ był w równowadze.
Tarcie ślizgowe – zadanie 1
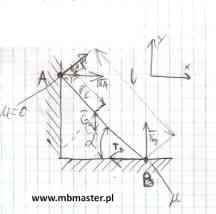
Przedmiotem przykładu jest drabina o masie m i długości l. Drabina jest oparta o ścianę w punkcie A oraz o podłogę w punkcie. Na styku drabiny z punktem A tracie ślizgowe(tracie przesuwne) nie występuje. W punkcie B drabina oddziałuje z podłożem poprzez tarcie ślizgowe, współczynnik tarcia ślizgowego drabiny w tym punkcie jest znany i wynosi μ. Celem zadania jest wyznaczenie maksymalnego kąta αmax jaki może tworzyć drabina względem podłoża aby pozostała w równowadze.
Tarcie ślizgowe – zadanie 2
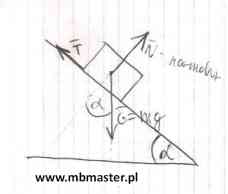
Na równi pochyłej o kącie nachylenia α znajduje się klocek. Klocek możemy potraktować jak punkt materialny, jego wymiary oraz kształt są zaniedbywalne w odniesieniu do otoczenia. Pomiędzy klockiem a powierzchnią równi występuje tracie ślizgowe o współczynniku μ. W zadaniu mamy wyznaczyć maksymalny kąt nachylenia równi αmax dla którego klocek pozostanie w spoczynku(nie wystąpi zjawisko ruchu).
Tarcie toczne – zadanie 1
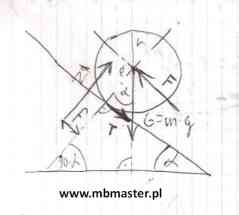
W tym przykładzie zajmować się będziemy analizą równowagi walca znajdującego się na równi pochyłej. Równia pochyła nachylona jest względem poziomu o kąt α. Masa walca wynosi m. Pomiędzy walcem a równią pochyłą występuje tracie toczne o współczynniku ƒ[m] oraz tarcie ślizgowe o współczynniku μ[-]. Należy pamiętać o tym że tarcie ślizgowe jest wielkością bezwymiarową, natomiast tarcie toczne posiada wymiar a jest nim [m](metr). Celem zadania jest wyznaczenie siły Fmax jaką musimy przyłożyć do środka ciężkości walca aby się nie stoczył z równi oraz aby nie zaczął na nią wyjeżdżać. Walec musi pozostać w spoczynku. Wskazówką niech będzie fakt, że gdy w zadaniu występuje tarcie toczne o współczynniku ƒ, to siłę oddziaływania podłoża na walec przesuwamy z miejsca styku walca z podłożem o odcinek równy współczynnikowi ƒ. Kierunek przesunięcia jest stronę zakładanego przez nas kierunku ruchu.