Zjawisko tarcia jest jednym z podstawowych oporów ruchu z jakim spotykamy się w mechanice. Tarcie jest oporem materii, która przeciwdziała ruchowi ciała umieszczonego w niej. Opór powietrza jest przykładem oporu materii. W mechanice najczęściej spotykamy się z dwoma rodzajami tarcia:
• tarciem przesuwnym (siła tarcia powstaje w wyniku przesuwania się po sobie powierzchni lub próby przesunięcia bez wykonania wprowadzenia w ruch)
• tarciem tocznym (opór podczas toczenia ciał)
Gdy tarcie nie występowało to na mocy pierwszej zasady dynamika Newtona ciało raz rozpędzone poruszałoby się ruchem jednostajnym w nieskończoność, gdyby na ciało działała niezrównoważona siła to na mocy drugiej zasady dynamiki Newtona ciało rozpędzałoby się w nieskończoność. Oczywiście jak wiemy z doświadczeń oba hipotetyczne przypadki nie występują. Pierwszy przypadek jest niemożliwy z uwagi na występowanie oporu materii, a drugi przypadek z powodu oporu materii oraz ograniczeń związanych Szczególną Teorią Względności Alberta Einsteina (żadne ciało posiadające masę spoczynkową większą od zera, nie może osiągnąć prędkości większej od prędkości światła c w próżni).
Tarcie opisane jest prawami tarcia. Prawa tarcia zostały wyznaczone doświadczalnie.
• siła tarcia jest zawsze przeciwna do występującego lub zakładanego kierunku ruchu
• wartość siły tarcia nie zależy od pola powierzchni stykających się ciał, zależy od rodzaju tych powierzchni
• siła tarcia T związana jest siłą nacisku N równaniem T=μ·N
• dla małych prędkości względnych, siła tarcia jest niezależna od prędkości

Tarcie przesuwne podzielone jest na:
• tarcie przesuwne statyczne μ_s[-]
• tarcie przesuwne kinetyczne opisane współczynnikiem μ_k[-]
Jak można wnioskować z nazewnictwa rodzajów tarć przesuwnych, przy tarciu przesuwnym statycznym ruch nie występuje μ_s[-], natomiast tarcie przesuwne kinetyczne μ_s[-] występuje podczas ruchu. Współczynniki tarć przesuwnych są bezwymiarowe, ich wartości wyznaczane są doświadczalnie. Wartości współczynników tarcia dla różnych materiałów znaleźć można tablicach matematyczno-fizycznych. Zapamiętać należy fakt, że współczynnik tarcia przesuwnego statycznego ma zawsze większe wartość od współczynnika tarcia przesuwnego kinetycznego → μ_s>μ_k. Źródłem siły tarcia są „szczątkowe” oddziaływania elektromagnetyczne pomiędzy molekułami (atomami) stykających się powierzchni. Siła tarcia ma zawsze przeciwny zwrot do kierunku ruchu ciała, bądź zakładanego kierunku ruchu ciała.
Tarcie toczne (tarcie potoczyste) występuje podczas toczenia się ciał. Tarcie toczne występuje podczas toczenia, jest ono wynikiem odkształcania się stykających powierzchni podczas toczenia. Tarcie toczne opisane jest współczynnikiem ƒ[m]. Współczynnik tarcia tocznego nie jest wielkością bezwymiarową, posiada on wymiar a jest nim metr. W wyniku tarcia tocznego następuje przesunięcie siły nacisku N o odległość ƒ kierunku równoległym do siły nacisku jakby toczenie nie występowało. Siła nacisku N jest przesuwana o współczynnik tarcia tocznego ƒ w zakładanym kierunku występowania ruchu. Dzieląc współczynnik tarcia tocznego ƒ przez promień r toczącego się ciała można wprowadzić bezwymiarowy współczynik oporu przy toczeniu (współczynnik ten obowiązuje tylko dla danego promienia r) → (ƒ/r)=μ_t(r). Pomiędzy wprowadzonym przed chwilą bezwymiarowym współczynnikiem tarcia tocznego μ_t(r) a współczynnikami dla tarcia przesuwnego zachodzi nierówność μ_t(r)<μ_k<μ_s. Z nierówności wynika, że siła tarcia podczas toczenia jest zawsze mniejsza od tarcia przesuwnego(ślizgowego), tłumaczy to dlaczego od niepamiętnych czasów toczeniem zastępowano przesuwanie. Dla napędów wykorzystujących ruch obrotowy z siłą tarcia związany jest moment obciążający będący momentem biernym, ponieważ jego zwrot zależy od kierunku ruchu M_T=f(ω).

Tarcie ślizgowe – zadanie 1

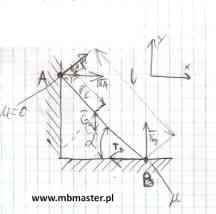
Przedmiotem przykładu jest drabina o masie m i długości l. Drabina jest oparta o ścianę w punkcie A oraz o podłogę w punkcie. Na styku drabiny z punktem A tracie ślizgowe(tracie przesuwne) nie występuje. W punkcie B drabina oddziałuje z podłożem poprzez tarcie ślizgowe, współczynnik tarcia ślizgowego drabiny w tym punkcie jest znany i wynosi μ. Celem zadania jest wyznaczenie maksymalnego kąta α_max jaki może tworzyć drabina względem podłoża aby pozostała w równowadze.

Tarcie ślizgowe – zadanie 1

Tarcie ślizgowe – zadanie 2

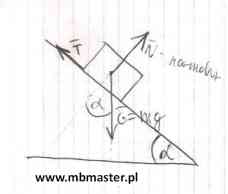
Na równi pochyłej o kącie nachylenia α znajduje się klocek. Klocek możemy potraktować jak punkt materialny, jego wymiary oraz kształt są zaniedbywalne w odniesieniu do otoczenia. Pomiędzy klockiem a powierzchnią równi występuje tracie ślizgowe o współczynniku μ. W zadaniu mamy wyznaczyć maksymalny kąt nachylenia równi α_max dla którego klocek pozostanie w spoczynku(nie wystąpi zjawisko ruchu).

Tarcie ślizgowe – zadanie 2

Tarcie ślizgowe – zadanie 3

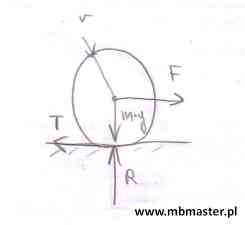
Jednorodny walce o masie m[kg] i promieniu r[m] leży na poziomym podłożu. Walec znajduje się w stanie spoczynku, jego prędkość początkowa v₀=0[m/s²]. Pomiędzy powierzchnią podłoża a powierzchnią styku walca występuje tarcie przesuwne kinetyczne o współczynniku μ_k. Walec znajduje się w idealnej próżni, pominięty zostaje więc opór powietrza. W pewnej chwili na środek masy walca zaczyna działa siła F[N]. Pod wpływem siły F walec zaczyna się przesuwać po powierzchni podłoża zgodnie z zwrotem siły F oraz przyśpieszeniem a. Przyśpieszenie a wyznaczone zostanie z drugiej zasady dynamiki Newtona. Celem zadania jest wyznaczenie prędkości końcowej walca v po pokonaniu przez niego drogi s=2·π·r[m].

Tarcie ślizgowe – zadanie 3

Tarcie toczne – zadanie 1

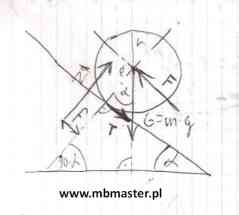
W tym przykładzie zajmować się będziemy analizą równowagi walca znajdującego się na równi pochyłej. Równia pochyła nachylona jest względem poziomu o kąt α. Masa walca wynosi m. Pomiędzy walcem a równią pochyłą występuje tracie toczne o współczynniku ƒ[m] oraz tarcie ślizgowe o współczynniku μ[-]. Należy pamiętać o tym że tarcie ślizgowe jest wielkością bezwymiarową, natomiast tarcie toczne posiada wymiar a jest nim [m](metr). Celem zadania jest wyznaczenie siły F_max jaką musimy przyłożyć do środka ciężkości walca aby się nie stoczył z równi oraz aby nie zaczął na nią wyjeżdżać. Walec musi pozostać w spoczynku. Wskazówką niech będzie fakt, że gdy w zadaniu występuje tarcie toczne o współczynniku ƒ, to siłę oddziaływania podłoża na walec przesuwamy z miejsca styku walca z podłożem o odcinek równy współczynnikowi ƒ. Kierunek przesunięcia jest stronę zakładanego przez nas kierunku ruchu.

Tarcie toczne – zadanie 1

Tarcie toczne – zadanie 2

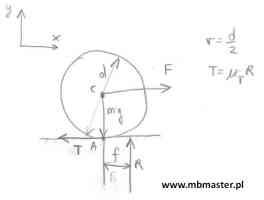
Jednorodny walec o promieniu r[m] i masie m[kg], leży na poziomym podłożu. Walec znajduje się w spoczynku. Pomiędzy powierzchnią styku walca z podłożem występuje tarcie toczne o współczynniku ƒ[m]. W środku masy walca działa siła F[N]. W przykładzie należy wyznaczyć maksymalną dopuszczalną wartość siły F_max, która nie spowoduje wytrącenia walca z stanu równowagi. W zadaniu zapisane zostaną równania równowagi statycznej dla rozważanego układu.

Tarcie toczne – zadanie 2

Tarcie toczne – zadanie 3

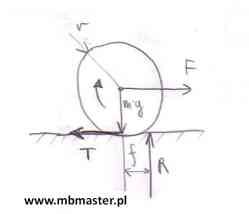
Jednorodny walce o masie m[kg] i promieniu r[m] leży na poziomym podłożu. Walec znajduje się w stanie spoczynku, jego prędkość początkowa v₀=0[m/s²]. Pomiędzy powierzchnią podłoża a powierzchnią styku walca występuje toczne o współczynniku ƒ[m]. Walec znajduje się w idealnej próżni, pominięty zostaje więc opór powietrza. W pewnej chwili na środek masy walca zaczyna działa siła F[N]. Pod wpływem siły F walec zaczyna się toczyć po powierzchni podłoża zgodnie z zwrotem siły F oraz przyśpieszeniem a. Przyśpieszenie a wyznaczone zostanie z drugiej zasady dynamiki Newtona. Walec tocząc się po podłożu wykonuje ruch płaski. Ruch płaski jest złożeniem ruchu postępowego i obrotowego. Celem zadania jest wyznaczenie prędkości końcowej walca v po pokonaniu przez niego drogi s=2·π·r[m].

Tarcie toczne – zadanie 3