Zjawisko tarcia jest jednym z podstawowych oporów ruchu z jakim spotykamy się w mechanice. Tarcie jest oporem materii, która przeciwdziała ruchowi ciała umieszczonego w niej. Opór powietrza jest przykładem oporu materii. W mechanice najczęściej spotykamy się z dwoma rodzajami tarcia:
• tarciem przesuwnym (siła tarcia powstaje w wyniku przesuwania się po sobie powierzchni lub próby przesunięcia bez wprowadzenia w ruch)
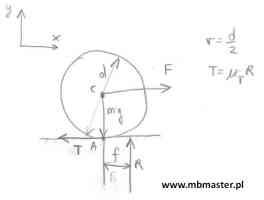
• tarciem tocznym (opór podczas toczenia ciał)
Gdy tarcie nie występowało to na mocy pierwszej zasady dynamika Newtona ciało raz rozpędzone poruszałoby się ruchem jednostajnym w nieskończoność, gdyby na ciało działała niezrównoważona siła to na mocy drugiej zasady dynamiki Newtona ciało rozpędzałoby się w nieskończoność. Oczywiście jak wiemy z doświadczeń oba hipotetyczne przypadki nie występują. Pierwszy przypadek jest niemożliwy z uwagi na występowanie oporu materii, a drugi przypadek z powodu oporu materii oraz ograniczeń związanych Szczególną Teorią Względności Alberta Einsteina (żadne ciało posiadające masę spoczynkową większą od zera, nie może osiągnąć prędkości większej od prędkości światła c w próżni).

Mechanika tarcie – zadania