Drgania harmoniczne są jednym z podstawowych zjawisk z jakimi mamy do czynienie w przyrodzie. W bardzo dużym skrócie można powiedzieć, ze wszystko drga. Każde ciało stałe wykonuje drgania, których częstotliwość nazywa się częstotliwością drgań własnych. Gdyby zacząć działać na ciało siłą wymuszającą o częstotliwości równej częstotliwości drgań własnych ciała to doprowadzi się je do zjawiska rezonansu mechanicznego. Oczywiście zjawisko rezonansu nie jest zarezerwowane tylko dla oddziaływań mechanicznych, występuje ono również w innych oddziaływaniach fizycznych. Przykładem jest rezonans elektryczny, szeroko stosowany w radioodbiornikach. Praktyczne jego zastosowanie polega na zwiększaniu się amplitudy interesującego nas sygnału dla sprecyzowanej częstotliwości. Układ wykonujący drgania harmoniczne porusza ruchem harmonicznym. Gdy siła działająca na ciało jest wprost proporcjonalna do wychylenia od pozycji równowagi to dany obiekt porusza się ruchem harmonicznym..
Oscylator harmoniczny prosty

Oscylator harmoniczny prosty zbudowany jest z masy punktowej m[kg] zawieszonej na sprężynie o sztywności k[N/m]. Oscylator harmoniczny wychylony z swojej pozycji równowagi o odległość Δx, a następnie po puszczeniu go rozpoczyna wykonywanie drgań harmonicznych nietłumionych. Oczywiście mówimy o sytuacji modelowej, ponieważ zakładamy że w układzie nie ma żadnych strat energii. Zakładamy że ruch odbywa się w idealnej próżni → brak oporu powietrza(oporu materii → tracie, lepkość). Zakładamy również że oscylator nie znajduje się również pod wpływem pola grawitacyjnego. W przykładzie rozwiążemy równanie ruchu oscylatora harmonicznego. Równanie ruchu jest równaniem różniczkowym. Wyznaczony zostanie także okres drgań harmonicznych oscylatora.
Oscylator harmoniczny tłumiony

Oscylator harmoniczny tłumiony zbudowany jest z masy punktowej m[kg] zawieszonej na sprężynie o sztywności k[N/m] oraz o współczynniku tłumienia l[N·s/m]. Oscylator harmoniczny wychylony z swojej pozycji równowagi o odległość Δx, a następnie po puszczeniu go rozpoczyna wykonywanie drgań harmonicznych tłumionych. Zakładamy że oscylator nie znajduje się pod wpływem pola grawitacyjnego. W przykładzie rozwiążemy równanie ruchu oscylatora harmonicznego podczas wykonywania drgań tłumionych. Równanie ruchu jest równaniem różniczkowym drugiego rzędu. Przeanalizowany zostanie także wpływ parametrów stałych jak masa m, sztywność k oraz współczynnik tłumienia l na charakter ruchu harmonicznego podczas tłumionych drgań harmonicznych.
Oscylator harmoniczny tłumiony
Wahadło matematyczne

Wahadło matematyczne zbudowane jest z nieważkiej nici o długości l. Jeden z końców nici przymocowany jest do sufitu. Do drugiego końca nici przymocowany jest punkt materialny o masie m. Punkt materialny jest przymocowany do sufitu poprzez nić. W stanie równowagi statycznej wahadło matematyczne znajduje się w spoczynku. W stanie równowagi siła grawitacji zrównoważona jest przez siłę naciągu nici. W pewnej chwili wahadło matematyczne zostało wychylone z pozycji równowagi o kąt α. Wahadło matematyczne znajduje się w polu grawitacyjnym Ziemi. Po wychyleniu z pozycji równowagi siła grawitacji rozkładana jest na dwie składowe. Pierwsza składowa siły grawitacji jest równoległa do punktu materialnego. Druga składowa jest prostopadła do punktu materialnego oraz to jego trajektorii ruchu. Obie składowe siły grawitacji są zależne od kąta α. W rozważanym przykładzie zakładamy brak oporu powietrza, ruch odbywa się w idealnej próżni. Wahadło matematyczne po wytrąceniu z położenia równowagi wykonuje ruch harmoniczny po okręgu.
Wahadło fizyczne

Wahadło fizyczne jest bryłą sztywną. Jeden z końców bryły sztywnej przymocowany jest za pomocą przegubu do sufitu. Bryła sztywna może się obracać wokół osi obrotu przegubu. Oś obrotu jest prostopadła do płaszczyzny rysunku. Bryła sztywana posiada masę m i moment bezwładności I. Długość bryły sztywnej wynosi 2·l. Moment bezwładności I jest znany dla osi obrotu. W stanie równowagi bryła sztywna się nie porusza (znajduje się w stanie spoczynku). W stanie równowagi siła grawitacji działająca na bryłę jest równoważona przez siły reakcji. W pewnej chwili bryła została wychylona z pozycji równowagi o kąt α. Bryła znajduje się w polu grawitacyjnym Ziemi. Wahadło fizyczne jest bryłą sztywną, więc siła grawitacji jest umieszczona w punkcie środka masy C. Po wychyleniu z pozycji równowagi siła grawitacji rozkładana jest na dwie składowe. Pierwsza składowa siły grawitacji jest równoległa do osi bryły. Druga składowa jest prostopadła do osi bryły oraz to jej trajektorii ruchu. Obie składowe siły grawitacji są zależne od kąta α. W rozważanym przykładzie zakładamy brak oporu powietrza, ruch odbywa się w idealnej próżni. Wahadło fizyczne po wytrąceniu z położenia równowagi wykonuje ruch harmoniczny.
Drgania harmonicze – zadanie 1

Walec o masie m zanurzony jest w płynie o gęstości ρ. W chwili początkowej walec znajduje się w stanie równowagi. Po chwili następuje wytrącenie walca z równowagi poprzez przesunięcie go w kierunku pionowym o Δx. W rozpatrywanym przykładzie lepkość cieczy uznajemy za możliwą do zaniedbania oraz zakładamy że nie ma strat energii. Celem przykładu jest wyznaczenie okresu drgań harmonicznych.
Drgania harmoniczne walca zanurzonego w płynie
Drgania harmonicze – zadanie 2
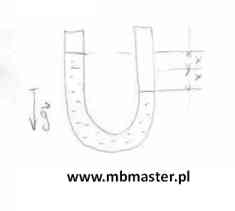
Rurka w kształcie litery U(U-rurka) wypełniona jest cieczą o gęstości ρ. Przekrój poprzeczny U-rurki wynosi S. Następnie w jednym z ramion rurki ciecz zostaje wypchnięta z położenia równowagi o odcinek Δx. W wyniku wytrącenia z równowagi ciecz w U-rurce wykonuje drgania harmoniczne. W rozwiązanym tutaj przykładzie wyznaczamy okres drgań harmonicznych.
Drgania harmoniczne cieczy w U-rurce
Drgania harmonicze – zadanie 3

Belka o masie m1 umieszczona jest na ruchomych walcach. Walce posiadają jednakowe masy równe m2. Środki walców umieszczone są w odległości 2·l[m] od siebie. Walce wirują wokół z jednakową co do wartości prędkością kątową ω[rad/s]. Kierunki wirowania walców są różne. Pomiędzy spodem belki a walcami występuje tarcie ślizgowe opisane współczynnikiem ƒ[-]. W pewnej chwili belka zostaje wypchnięta z położenia równowagi o odcinek Δx. Belka jest bryłą sztywną, siła grawitacji działa więc na nią w miejscu jest środka ciężkości C. Po wytrąceniu z położenia równowagi belka zaczyna wykonywać drgania harmoniczne. W zadaniu wyznaczony zostaje okres drgań harmonicznych belki.