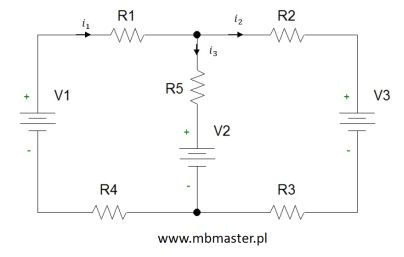
Wyznaczanie równań Kirchhoffa dla obwodu elektrycznego. Obwód elektryczny zbudowany jest ze źródeł napięcia, źródeł prądu oraz rezystorów. Liczba równań Kirchhoffa niezbędna do rozwiązania obwodu elektrycznego jest następująca:
Liczbę węzłów oznaczamy jako n , stosując równania Kirchhoffa do rozwiązania obwodu elektrycznego liczba równań dla pierwszego prawa Kirchhoffa jest równa (n – 1):

I. K \rightarrow (n - 1)

Liczba równań napięciowych Kirchhoffa jest zależna od liczby gałęzi i węzłów w obwodzie. Wzór ogólny dla liczby równań napięciowych jest postaci:

II. K \rightarrow m - (n - 1)

gdzie:
m – liczba gałęzi
n – liczba węzłów

Równanie prądowe Kirchhoffa dla węzła „1” i „2”:

I_1 - I_2 - I_3 + I_{z1} = 0

Równanie prądowe Kirchhoffa dla węzła „3” i „4”:

I_2 + I_3 - I_{z1} - I_5 - I_4 - I_{z2} = 0

Równanie napięciowe Kirchhoffa dla oczka nr 1:

V_{z1} - R_1 \cdot I_1 - R_2 \cdot I_2 + V_{z3} + V_{z2} = 0 = 0

Równanie napięciowe Kirchhoffa dla oczka nr 2:

-V_{z2} - R_4 \cdot I_4 = 0 = 0

Równanie napięciowe Kirchhoffa dla oczka nr 3:

-V_{z3} + R_2 \cdot I_2 - R_3 \cdot I_3= 0 = 0

Pełne rozwiązanie rozpatrywanego przykładu:

Obwód elektryczny prądu stałego – prawa Kirchhoffa