Obwód elektroniczny z diodą

Elektronika, Elektrotechnika, Obwody elektryczne,

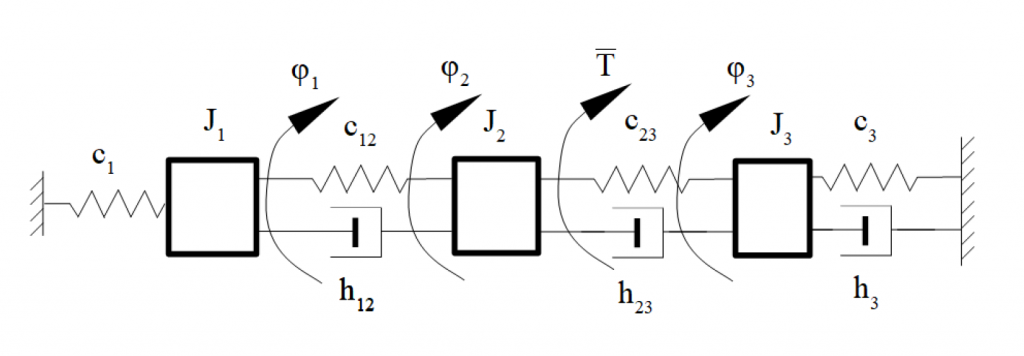
W przykładzie rozpatrzony zostanie obwód elektroniczny z diodą krzemową. Rozpatrywany obwód zbudowany jest z dwóch oczek. W celu wyznaczenia prądów w obwodzie wyznaczone zostaną równania dla pierwszego i drugiego prawa Kirchhoffa.

Równanie prądowe Kirchhoffa
i - i_1 - i_2 = 0

Równanie napięciowe Kirchhoffa dla pierwszego oczka
V_1 - i \cdot R_1 - i_2 \cdot R_2 = 0

Równanie napięciowe Kirchhoffa dla drugiegooczka
i_2 \cdot R_2 - U_d - i_1 \cdot R_3 = 0

Pełne rozwiązanie analizowanego przykładu zadanie z diodą.

Równania Lagrange’a dla układu mechanicznego

Dynamika, Mechanika,

Dynamika trójmasowego układu mechanicznego w ruchu obrotowym. W rozważanym przykładzie zastosowane zostanie zapis energii w formie wariacyjnej tj. innymi słowy w postaci równań Eulera-Lagrange’a pierwszego rodzaju.

Trójmasowy układ mechaniczny

Ogólna postać równań Lagrange’a
L = E_k - V

Równania Lagrange’a pierwszego rodzaju:

\frac{d}{dt}\frac{\partial{L}}{\partial{{\dot{q_i}}}} - \frac{\partial{L}}{\partial{q_i}} + \frac{\partial{D}}{\partial{{\dot{q_i}}}} = \sum_{k}{Q_{k}}

Znaczenie symboli:

L \rightarrow Lagrangian E_k \rightarrow energia \,kinetyczna V \rightarrow energia \,potencjalna D \rightarrow \,dyssypacja \,energii q_i \rightarrow zmienna \,o \,indeksie \,i \dot{ q_i} \rightarrow pierwsza \,pochodna \,po \,czasie

Zmienne w rozważanym układzie mechanicznym:

q_1 = \varphi_1, \dot q_1 =\dot \varphi_1 q_2 = \varphi_2, \dot q_2 =\dot \varphi_2 q_3 = \varphi_3, \dot q_3 =\dot \varphi_3

Energia kinetyczna:

E_k = \frac{1}{2}\cdot J_1 \cdot \dot{\varphi_1}^2 + \frac{1}{2}\cdot J_2 \cdot \dot{\varphi_2}^2 + \frac{1}{2}\cdot J_3 \cdot \dot{\varphi_3}^2

Energia potencjalna:

V = \frac{1}{2}\cdot c_1 \cdot \varphi_{1}^2 + \frac{1}{2}\cdot c_{12} \cdot (\varphi_{2} - \varphi_{1})^2 + \frac{1}{2}\cdot c_{23} \cdot (\varphi_{2} - \varphi_{3})^2 + \frac{1}{2}\cdot c_3 \cdot \varphi_{3}^2

Dyssypacja energii:

D = \frac{1}{2}\cdot h_{12} \cdot (\dot\varphi_{2} - \dot\varphi_{1})^2 + \frac{1}{2}\cdot h_{23} \cdot (\dot\varphi_{2} - \dot\varphi_{3})^2 + \frac{1}{2}\cdot h_3 \cdot \dot\varphi_{3}^2

Równania dla zmiennej q1:

J_1 \cdot \ddot \varphi_1 - (-c_1 \cdot \varphi_1 - c_{12} \cdot (\varphi_2 - \varphi_1) \cdot (-1)) + (h_{12}\cdot (\dot \varphi_2 - \dot \varphi_1)\cdot (-1)) = 0
J_1 \cdot \ddot \varphi_1 + c_1 \cdot \varphi_1 - c_{12} \cdot (\varphi_2 - \varphi_1) - h_{12}\cdot (\dot \varphi_2 - \dot \varphi_1) = 0
J_1 \cdot \ddot \varphi_1 = - c_1 \cdot \varphi_1 + c_{12} \cdot (\varphi_2 - \varphi_1) + h_{12}\cdot (\dot \varphi_2 - \dot \varphi_1)

Równania dla zmiennej q2:

J_2 \cdot \ddot \varphi_2 - (-c_{12}\cdot (\varphi_2 - \varphi_1) -c_{23}\cdot (\varphi_2 - \varphi_3)) + (h_{12}\cdot (\dot\varphi_2 - \dot\varphi_1) + h_{23}\cdot (\dot\varphi_2 - \dot\varphi_3)) = T
J_2 \cdot \ddot \varphi_2 + c_{12}\cdot (\varphi_2 - \varphi_1) + c_{23}\cdot (\varphi_2 - \varphi_3) + h_{12}\cdot (\dot\varphi_2 - \dot\varphi_1) + h_{23}\cdot (\dot\varphi_2 - \dot\varphi_3) = T
J_2 \cdot \ddot \varphi_2 = - c_{12}\cdot (\varphi_2 - \varphi_1) - c_{23}\cdot (\varphi_2 - \varphi_3) - h_{12}\cdot (\dot\varphi_2 - \dot\varphi_1) - h_{23}\cdot (\dot\varphi_2 - \dot\varphi_3) + T

Równania dla zmiennej q3:

J_3 \cdot \ddot \varphi_3 - (-c_{23}\cdot (\varphi_2 - \varphi_3)\cdot(-1) -c_{3}\cdot \varphi_3) + (h_{23}\cdot (\dot\varphi_2 - \dot\varphi_3)\cdot(-1) + h_{3}\cdot \dot\varphi_3) = 0
J_3 \cdot \ddot \varphi_3 - c_{23}\cdot (\varphi_2 - \varphi_3) + c_{3}\cdot \varphi_3 - h_{23}\cdot (\dot\varphi_2 - \dot\varphi_3) + h_{3}\cdot \dot\varphi_3 = 0
J_3 \cdot \ddot \varphi_3 = c_{23}\cdot (\varphi_2 - \varphi_3) - c_{3}\cdot \varphi_3 + h_{23}\cdot (\dot\varphi_2 - \dot\varphi_3) - h_{3}\cdot \dot\varphi_3


Dynamika w ruchu obrotowym

Dynamika, Mechanika,

W przykładzie rozpatrzony zostanie układ mechaniczny o trzech stopniach swobody. W jednym miejscu układu przyłożony jest zewnętrzny moment T. Rozpatrywany układ posiada w swojej strukturze elementy sprężyste i tłumiące.

Układ mechaniczny o trzech stopniach swobody

Równanie dla pierwszego stopnia swobody:

J_{1}\cdot \ddot{\varphi_1} = -c_1\cdot\varphi_1 + c_{12}\cdot(\varphi_2 - \varphi_1) + h_{12}\cdot(\dot{\varphi_2} - \dot{\varphi_1})

Równanie dla drugiego stopnia swobody

J_{2}\cdot \ddot{\varphi_2} = -c_{12}\cdot(\varphi_2 - \varphi_1) - h_{12}\cdot(\dot{\varphi_2} - \dot{\varphi_1}) - c_{23}\cdot(\varphi_2 - \varphi_3) - h_{23}\cdot(\dot{\varphi_2} - \dot{\varphi_3}) + T

Równanie dla trzeciegostopnia swobody

J_{3}\cdot \ddot{\varphi_3} = -c_3\cdot\varphi_3 - h_3\cdot\dot\varphi_3+ c_{23}\cdot(\varphi_2 - \varphi_3) + h_{23}\cdot(\dot{\varphi_2} - \dot{\varphi_3})

Admitancja równoległego połączenie elementów R, L, C

Elektrotechnika, Obwody elektryczne,
Obwód elektryczny RLC

Dla rozważanego obwodu elektrycznego RLC wyznaczona zostanie admitancja.

\underline{Y} = \frac{1}{\underline {Z}}

Jednostka admitancji jest Siemens.

S = \frac{1}{\Omega} = \Omega^{-1}

Wyznaczenie admitancji \underline{Y} widzianej od strony zacisków A i B sprowadza się wyznaczenia sumy admitancji składowych tj.

\underline{Y} = \underline{Y} _R + \underline{Y} _L + \underline{Y} _C

Pełne rozwiązanie przykładu – impedancja zadanie 6

Prawa Kirchhoffa w obwodach elektrycznych

Elektronika, Elektrotechnika, Obwody elektryczne,
Obwód elektryczny prądu stałego

Wyznaczanie równań Kirchhoffa dla obwodu elektrycznego. Obwód elektryczny zbudowany jest ze źródeł napięcia, źródeł prądu oraz rezystorów. Liczba równań Kirchhoffa niezbędna do rozwiązania obwodu elektrycznego jest następująca:
Liczbę węzłów oznaczamy jako n , stosując równania Kirchhoffa do rozwiązania obwodu elektrycznego liczba równań dla pierwszego prawa Kirchhoffa jest równa (n – 1):

I. K \rightarrow (n - 1)

Liczba równań napięciowych Kirchhoffa jest zależna od liczby gałęzi i węzłów w obwodzie. Wzór ogólny dla liczby równań napięciowych jest postaci:

II. K \rightarrow m - (n - 1)

gdzie:
m – liczba gałęzi
n – liczba węzłów

Równanie prądowe Kirchhoffa dla węzła „1” i „2”:

I_1 - I_2 - I_3 + I_{z1} = 0

Równanie prądowe Kirchhoffa dla węzła „3” i „4”:

I_2 + I_3 - I_{z1} - I_5 - I_4 - I_{z2} = 0

Równanie napięciowe Kirchhoffa dla oczka nr 1:

V_{z1} - R_1 \cdot I_1 - R_2 \cdot I_2 + V_{z3} + V_{z2} = 0 = 0

Równanie napięciowe Kirchhoffa dla oczka nr 2:

-V_{z2} - R_4 \cdot I_4 = 0 = 0

Równanie napięciowe Kirchhoffa dla oczka nr 3:

-V_{z3} + R_2 \cdot I_2 - R_3 \cdot I_3= 0 = 0

Pełne rozwiązanie rozpatrywanego przykładu:

Obwód elektryczny prądu stałego – prawa Kirchhoffa

Moment bezwładności

Mechanika,

Moment bezwładności jest odpowiednikiem masy w ruchu obrotowym.

W ogólności moment bezwładności dany jest wzorem:

I = \int_m r^2 \cdot dm

Moment bezwładności bryły sztywnej jest więc sumą iloczynów elementarnych mas dm i kwadratu ich odległości od osi obrotu.

Bardzo często przy obliczaniu momentów bezwładności wykorzystywane jest twierdzenie o osiach równoległych, znane również jako Twierdzenie Steinera.


I = I_0 + m \cdot d^2

Rozwiązane zadania i przykłady:

Moment bezwładności

Układ elektroniczny z diodą krzemową

Elektronika, Elektrotechnika, Obwody elektryczne, ,
Układ elektroniczny z diodą krzemową

W zamieszczonym przykładzie obwodu elektronicznego zbudowane z źródła napięcia, rezystora i diody krzemowej wyznaczone zostanie równanie napięciowe Kirchhoffa. W oparciu o równanie napięciowe obliczony zostanie prąd elektryczny płynący w obwodzie elektronicznym.

Równanie napięciowe Kirchhoffa

V_1 - i\cdot R_1 - U_{D1} = 0

Równanie opisujące prąd elektryczny w obwodzie

i = \frac{V_1 - U_{D1}}{R_1}

Pełne rozwiązanie przedstawionego zadania układ elektroniczny z diodą krzemową.

Tarcie toczne

Mechanika, Statyka

Tarcie toczne

Wałek o masie m posiada możliwość toczenia się z równi pochyłej. Promień przekroju poprzecznego wałka wynosi r. Celem zadania jest wyznaczenie siły F, którą należy przyłożyć w środku masy wałka tak aby pozostał on w równowadze. Pomiędzy wałkiem a równią występuje tarcie toczne o współczynniku f.

\Sigma F_{ix} = 0 -F + G\cdot sin{\alpha} + T= 0 \Sigma F_{iy} = 0 N - G\cdot cos{\alpha}= 0 \Sigma M_{ia} = 0 -f\cdot N+ r\cdot T= 0

Pełne rozwiązanie przykładu przedstawionego powyżej – tarcie toczne zadanie.

Drgania masy na sprężynie

Dynamika, Mechanika, ,

Wyznaczanie równania ruchu dla masy drgającej na sprężynie. W rozważanym układzie kula o masie m [kg] jest przytwierdzona do sufitu za pomocą sprężyny o sztywności k [\frac{N}{m}].

Masa drgająca

Równanie ruchu dla rozważanego układu jest postaci:

m \cdot \vec{a} = -k\cdot \vec{x}

Rozważane równanie ruchu jest równaniem różniczkowym pierwszego rzędu o zmiennych rozdzielonych.

m \cdot \frac{d^2x}{dt^2} = -k\cdot x

Stosując zapis Newton-a tj. oznaczając kolejne pochodne względem czasu poprzez kropki nad różniczkowaną zmienną, równanie ruchu ma postać:

m \cdot \ddot x = -k\cdot x

Oscylator harmoniczny prosty

Wzmacniacz operacyjny w konfiguracji odwracającej

Automatyka, Elektronika, Wzmacnicze operacyjne

Wzmacniacze operacyjne są jednymi z podstawowych układów elektronicznych. W zależności od konfiguracji, układy wzmacniacza mogą realizować różne operacje na sygnale wejściowym. W rezultacie sygnał wyjściowy wzmacniacza operacyjnego jest przetworzonym sygnałem wejściowym.

Dla wzmacniacza w konfiguracji odwracającej zależność pomiędzy sygnałem wyjściowym i wejściowym jest następująca:

V_{out}(t) = -\frac{R_F}{R_1} \cdot V_{in}(t)

Pełne wyprowadzenie zależności powyżej znaleźć można tutaj:

Wzmacniacz operacyjny w konfiguracji odwracającej